Chủ đề bài tập lực hấp dẫn: Bài viết này cung cấp một loạt các bài tập về lực hấp dẫn, giúp bạn khám phá sâu hơn về khái niệm này trong vật lý. Từ các bài tập cơ bản đến nâng cao, nội dung được thiết kế nhằm rèn luyện kỹ năng và củng cố kiến thức, đồng thời giải thích chi tiết và dễ hiểu để hỗ trợ bạn trong quá trình học tập.
Mục lục
Bài tập lực hấp dẫn
Lực hấp dẫn là một khái niệm cơ bản trong vật lý học, đóng vai trò quan trọng trong việc hiểu các hiện tượng tự nhiên. Dưới đây là các bài tập liên quan đến lực hấp dẫn kèm theo lời giải chi tiết.
Công thức lực hấp dẫn
Lực hấp dẫn giữa hai vật được xác định bằng công thức:
$$ F = G \cdot \frac{{m_1 \cdot m_2}}{{r^2}} $$
- F: Lực hấp dẫn (N)
- G: Hằng số hấp dẫn (6,674 × 10-11 N·(m/kg)2)
- m1, m2: Khối lượng của hai vật (kg)
- r: Khoảng cách giữa hai vật (m)
Bài tập minh họa
Bài tập 1: Tính lực hấp dẫn giữa hai vật
Cho hai vật có khối lượng lần lượt là 5 kg và 10 kg, khoảng cách giữa chúng là 2 m. Hãy tính lực hấp dẫn giữa hai vật này.
Lời giải:
Áp dụng công thức:
$$ F = 6,674 \times 10^{-11} \cdot \frac{{5 \times 10}}{{2^2}} $$
$$ F = 8,3425 \times 10^{-10} N $$
Bài tập 2: Tác động của trọng lực
Một vật có khối lượng 2 kg rơi từ độ cao 10 m. Tính lực tác động của trọng lực lên vật.
Lời giải:
Lực tác động được tính bằng:
$$ F = m \cdot g $$
Với gia tốc trọng trường \( g \approx 9,8 m/s^2 \), ta có:
$$ F = 2 \times 9,8 = 19,6 N $$
Bài tập thực hành
- Tính lực hấp dẫn giữa hai vật có khối lượng 3 kg và 7 kg cách nhau 1,5 m.
- Một vệ tinh có khối lượng 500 kg đang quay quanh Trái Đất ở độ cao 400 km. Tính lực hấp dẫn tác dụng lên vệ tinh.
- Hai quả cầu nhỏ cách nhau 0,5 m có khối lượng lần lượt là 0,2 kg và 0,5 kg. Hãy xác định lực hấp dẫn giữa chúng.
Kết luận
Những bài tập về lực hấp dẫn giúp củng cố kiến thức về định luật vạn vật hấp dẫn của Newton, đồng thời rèn luyện kỹ năng tính toán và áp dụng công thức vào các bài toán thực tiễn.

.png)
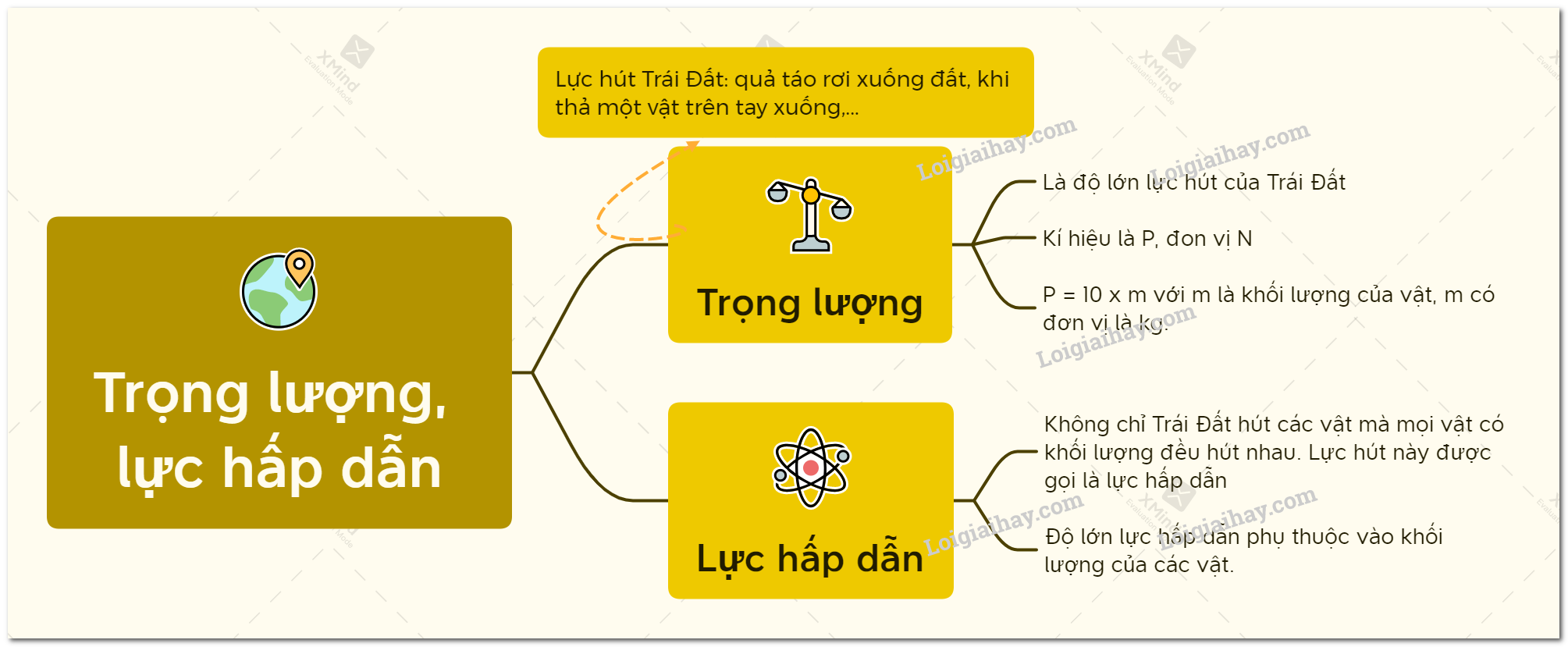
Giới thiệu về lực hấp dẫn
Lực hấp dẫn là một trong bốn lực cơ bản của tự nhiên, bên cạnh lực điện từ, lực hạt nhân mạnh và lực hạt nhân yếu. Lực này được Isaac Newton phát hiện và mô tả chi tiết trong thế kỷ 17. Định luật vạn vật hấp dẫn của Newton đã đặt nền móng cho hiểu biết của con người về cách các vật thể tương tác với nhau trong vũ trụ.
Lực hấp dẫn là lực hút giữa hai vật có khối lượng, được xác định bằng công thức:
$$ F = G \cdot \frac{{m_1 \cdot m_2}}{{r^2}} $$
- F: Lực hấp dẫn giữa hai vật (N).
- G: Hằng số hấp dẫn (6,674 × 10-11 N·m2/kg2).
- m1, m2: Khối lượng của hai vật (kg).
- r: Khoảng cách giữa hai vật (m).
Lực hấp dẫn không chỉ giữ cho các hành tinh quay quanh Mặt Trời mà còn là lực chính yếu giữ các thiên hà và vũ trụ với nhau. Mặc dù lực hấp dẫn là lực yếu nhất trong bốn lực cơ bản, nhưng phạm vi tác dụng của nó là vô hạn và ảnh hưởng của nó có thể cảm nhận trên quy mô rất lớn.
Trong cuộc sống hàng ngày, lực hấp dẫn là lý do mà mọi vật đều rơi về phía Trái Đất khi không có lực nào khác ngăn cản. Nó cũng là nguyên nhân tạo ra trọng lực mà chúng ta cảm nhận hàng ngày, giữ cho chúng ta đứng vững trên mặt đất.
Hiểu biết về lực hấp dẫn không chỉ giúp giải thích các hiện tượng tự nhiên mà còn ứng dụng trong nhiều lĩnh vực khoa học và kỹ thuật, từ việc phóng vệ tinh đến dự báo thời tiết và khám phá vũ trụ.
Công thức và định luật liên quan đến lực hấp dẫn
Lực hấp dẫn là một trong những khái niệm quan trọng nhất trong vật lý, và nó được mô tả chi tiết qua định luật vạn vật hấp dẫn của Isaac Newton. Công thức cơ bản của lực hấp dẫn được sử dụng để tính toán lực hút giữa hai vật có khối lượng.
1. Định luật vạn vật hấp dẫn của Newton
Định luật này được phát biểu rằng: "Mọi hạt vật chất trong vũ trụ hút nhau với một lực tỷ lệ thuận với tích khối lượng của chúng và tỷ lệ nghịch với bình phương khoảng cách giữa chúng."
Công thức của định luật vạn vật hấp dẫn là:
$$ F = G \cdot \frac{{m_1 \cdot m_2}}{{r^2}} $$
- F: Lực hấp dẫn giữa hai vật (đơn vị: Newton, N).
- G: Hằng số hấp dẫn, có giá trị xấp xỉ 6,674 × 10-11 N·m2/kg2.
- m1, m2: Khối lượng của hai vật (đơn vị: kilogram, kg).
- r: Khoảng cách giữa tâm hai vật (đơn vị: meter, m).
2. Hằng số hấp dẫn (G)
Hằng số hấp dẫn (G) là một hằng số vật lý cơ bản, biểu thị độ mạnh của lực hấp dẫn trong công thức. Giá trị của G được xác định thông qua các thí nghiệm chính xác, và nó là yếu tố quan trọng trong việc tính toán lực hấp dẫn giữa hai vật.
3. Ứng dụng của định luật vạn vật hấp dẫn
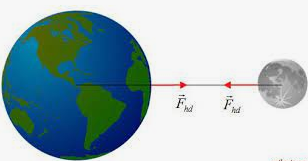
- Tính toán lực hút giữa các thiên thể trong vũ trụ, như giữa Trái Đất và Mặt Trăng.
- Dự đoán quỹ đạo của các hành tinh và vệ tinh nhân tạo.
- Giải thích hiện tượng rơi tự do và trọng lực trên Trái Đất.
Việc hiểu rõ công thức và định luật liên quan đến lực hấp dẫn giúp chúng ta có cái nhìn sâu sắc hơn về cách vũ trụ hoạt động và các hiện tượng tự nhiên xảy ra hàng ngày.

Bài tập lực hấp dẫn cơ bản
Để hiểu rõ hơn về lực hấp dẫn và áp dụng các định luật đã học, dưới đây là một số bài tập cơ bản giúp bạn thực hành.
1. Tính lực hấp dẫn giữa hai vật
Giả sử có hai vật có khối lượng lần lượt là 5 kg và 10 kg, đặt cách nhau 2 mét. Tính lực hấp dẫn giữa hai vật.
Bạn có thể áp dụng công thức:
$$ F = G \cdot \frac{{m_1 \cdot m_2}}{{r^2}} $$
- Bước 1: Xác định khối lượng của hai vật: \( m_1 = 5 \) kg, \( m_2 = 10 \) kg.
- Bước 2: Xác định khoảng cách giữa chúng: \( r = 2 \) m.
- Bước 3: Áp dụng giá trị của hằng số hấp dẫn \( G \approx 6,674 \times 10^{-11} \) N·m²/kg².
- Bước 4: Tính toán lực hấp dẫn \( F \).
2. Tính khoảng cách giữa hai vật
Biết rằng lực hấp dẫn giữa hai vật là 2 N, khối lượng của chúng lần lượt là 8 kg và 12 kg. Tính khoảng cách giữa hai vật.
Sử dụng công thức lực hấp dẫn:
$$ F = G \cdot \frac{{m_1 \cdot m_2}}{{r^2}} $$
- Bước 1: Xác định lực hấp dẫn \( F = 2 \) N, khối lượng \( m_1 = 8 \) kg, \( m_2 = 12 \) kg.
- Bước 2: Áp dụng giá trị của hằng số hấp dẫn \( G \approx 6,674 \times 10^{-11} \) N·m²/kg².
- Bước 3: Giải phương trình để tìm khoảng cách \( r \).
3. Tính khối lượng của một vật dựa trên lực hấp dẫn
Giả sử lực hấp dẫn giữa hai vật là 3 N và khối lượng của một vật là 7 kg. Tính khối lượng của vật còn lại nếu khoảng cách giữa hai vật là 1,5 mét.
Sử dụng công thức đã biết:
$$ F = G \cdot \frac{{m_1 \cdot m_2}}{{r^2}} $$
- Bước 1: Xác định các giá trị đã biết: \( F = 3 \) N, \( m_1 = 7 \) kg, \( r = 1,5 \) m.
- Bước 2: Áp dụng giá trị của hằng số hấp dẫn \( G \approx 6,674 \times 10^{-11} \) N·m²/kg².
- Bước 3: Giải phương trình để tìm khối lượng \( m_2 \).
Những bài tập trên giúp củng cố kiến thức về lực hấp dẫn, cách sử dụng công thức liên quan và khả năng áp dụng trong các tình huống khác nhau.

Bài tập lực hấp dẫn nâng cao
Bài tập lực hấp dẫn nâng cao giúp học sinh hiểu sâu hơn về các nguyên lý và ứng dụng của lực hấp dẫn trong vũ trụ. Dưới đây là một số bài tập cụ thể mà bạn có thể tham khảo:
Bài tập 1: Tính lực hấp dẫn trong không gian vũ trụ
Cho hai vật thể A và B có khối lượng lần lượt là \(m_A = 5 \, kg\) và \(m_B = 10 \, kg\) nằm cách nhau một khoảng \(d = 2 \, m\) trong không gian vũ trụ.
- Áp dụng định luật vạn vật hấp dẫn của Newton để tính lực hấp dẫn giữa hai vật thể.
- Công thức tính lực hấp dẫn:
- Thay giá trị cụ thể vào công thức:
- Tính toán kết quả và so sánh với lực hấp dẫn trên Trái Đất.
\[ F = G \times \frac{m_A \times m_B}{d^2} \]
\[ F = 6.674 \times 10^{-11} \times \frac{5 \times 10}{2^2} \, N \]
Bài tập 2: Bài toán quỹ đạo chuyển động của các thiên thể
Một vệ tinh nhân tạo có khối lượng \(m = 500 \, kg\) đang chuyển động trên quỹ đạo quanh Trái Đất ở khoảng cách \(r = 7000 \, km\) từ tâm Trái Đất.
- Xác định tốc độ cần thiết để vệ tinh duy trì quỹ đạo tròn quanh Trái Đất.
- Công thức tính tốc độ quỹ đạo:
- Thay giá trị cụ thể vào công thức:
- Tính toán kết quả và so sánh với tốc độ thoát của vệ tinh.
\[ v = \sqrt{\frac{G \times M_T}{r}} \]
\[ v = \sqrt{\frac{6.674 \times 10^{-11} \times 5.972 \times 10^{24}}{7000 \times 10^3}} \, m/s \]
Bài tập 3: Kết hợp lực hấp dẫn và các lực khác
Cho một vật thể có khối lượng \(m = 2 \, kg\) đang rơi tự do dưới tác dụng của trọng lực trên Trái Đất. Xác định thời gian và vận tốc khi vật chạm đất từ độ cao \(h = 100 \, m\).
- Áp dụng công thức tính gia tốc trọng trường \(g\) và công thức chuyển động:
- Giải phương trình để tìm thời gian rơi và vận tốc khi chạm đất:
- Thay giá trị cụ thể vào công thức và tính toán kết quả.
\[ v = g \times t \]
\[ h = \frac{1}{2} \times g \times t^2 \]
\[ t = \sqrt{\frac{2h}{g}} \]
\[ v = g \times \sqrt{\frac{2h}{g}} \]
Những bài tập trên sẽ giúp bạn nắm vững kiến thức về lực hấp dẫn và khả năng áp dụng vào các bài toán thực tế.

Ứng dụng của lực hấp dẫn trong đời sống
Lực hấp dẫn không chỉ là một khái niệm lý thuyết, mà còn có nhiều ứng dụng quan trọng trong đời sống hàng ngày và các lĩnh vực khoa học khác nhau. Từ việc giữ chúng ta trên mặt đất đến sự chuyển động của các thiên thể trong vũ trụ, lực hấp dẫn đóng vai trò không thể thiếu.
Lực hấp dẫn và sự hình thành các hành tinh
Trong quá trình hình thành các hành tinh và ngôi sao, lực hấp dẫn là yếu tố chính giúp gắn kết các hạt vật chất lại với nhau. Qua hàng triệu năm, các hạt này tụ lại thành những khối lớn hơn, dần dần hình thành các hành tinh và thiên thể trong vũ trụ. Lực hấp dẫn cũng giúp duy trì quỹ đạo của các hành tinh xung quanh ngôi sao trung tâm, như Trái Đất quay quanh Mặt Trời.
Ứng dụng của lực hấp dẫn trong kỹ thuật và công nghệ
- Thiết kế quỹ đạo vệ tinh: Lực hấp dẫn được sử dụng để tính toán và thiết kế quỹ đạo của các vệ tinh nhân tạo quanh Trái Đất. Những tính toán này đảm bảo vệ tinh duy trì vị trí ổn định, thực hiện các nhiệm vụ viễn thám, liên lạc và nghiên cứu khoa học.
- Kỹ thuật hàng không: Trong ngành hàng không, lực hấp dẫn là một yếu tố quan trọng khi tính toán đường bay của máy bay và tên lửa. Việc hiểu rõ lực hấp dẫn giúp tối ưu hóa nhiên liệu và an toàn bay.
Lực hấp dẫn và các hiện tượng thiên nhiên
- Thủy triều: Lực hấp dẫn giữa Trái Đất và Mặt Trăng là nguyên nhân gây ra hiện tượng thủy triều, ảnh hưởng trực tiếp đến các hoạt động hàng hải và sinh thái ven biển.
- Sự di chuyển của dòng sông băng: Ở những vùng băng giá, lực hấp dẫn là yếu tố chính giúp di chuyển các dòng sông băng xuống dưới sườn núi, tạo nên các thung lũng băng và địa hình đặc trưng.
Như vậy, lực hấp dẫn không chỉ là một khái niệm trong vật lý mà còn có tác động sâu rộng đến nhiều khía cạnh của đời sống và khoa học, từ việc hình thành hành tinh đến các ứng dụng trong công nghệ và hiểu biết về thiên nhiên.