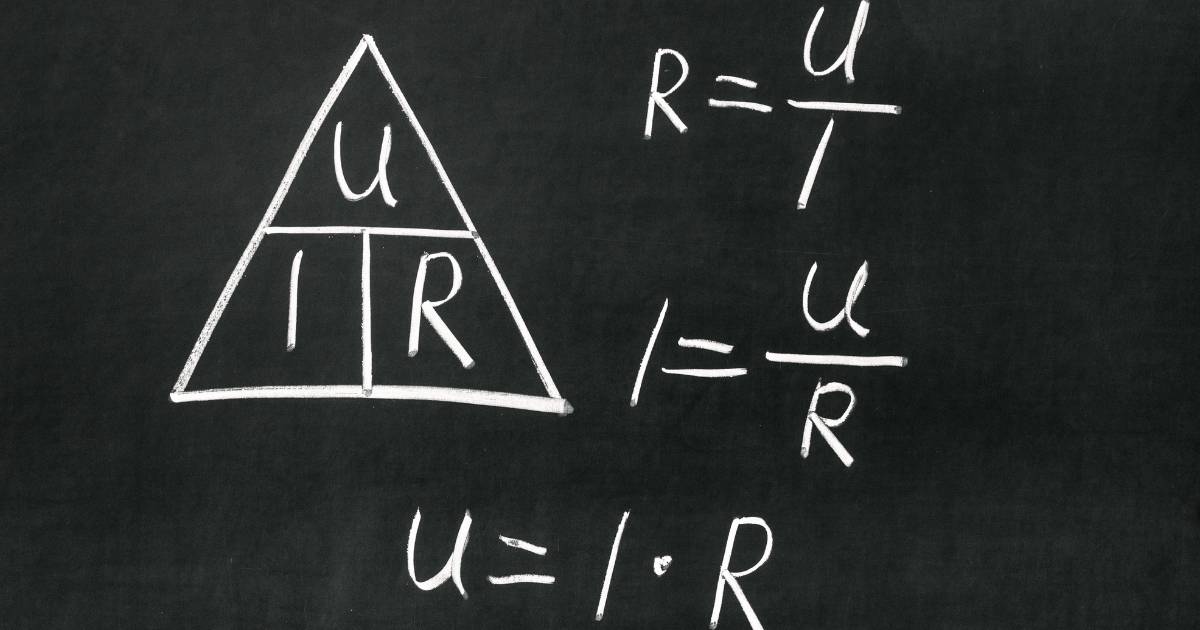Bài Tập Định Luật 2 Niu-tơn Nâng Cao: Phương Pháp Giải Và Ứng Dụng Thực Tế

Định luật 2 của Newton là một trong những nguyên lý cơ bản trong vật lý học, được áp dụng rộng rãi trong nhiều bài tập và ứng dụng thực tiễn. Việc hiểu rõ và làm chủ các bài tập liên quan đến định luật này giúp học sinh nắm vững kiến thức và phát triển tư duy logic. Dưới đây là một số thông tin và bài tập nâng cao về định luật 2 Newton.

1. Khái Quát Về Định Luật 2 Niu-tơn

Định luật 2 Niu-tơn phát biểu rằng gia tốc của một vật tỉ lệ thuận với lực tác dụng lên nó và tỉ lệ nghịch với khối lượng của vật. Phương trình cơ bản của định luật này là:

$$\vec{F} = m \cdot \vec{a}$$

Trong đó:

• F: Lực tác dụng lên vật (đơn vị: Newton, N)
• m: Khối lượng của vật (đơn vị: Kilogram, kg)
• a: Gia tốc của vật (đơn vị: mét trên giây bình phương, m/s²)

2. Các Dạng Bài Tập Nâng Cao

1. Bài tập về lực kéo và lực ma sát: Tính toán lực kéo cần thiết để di chuyển một vật trên mặt phẳng nghiêng có ma sát.
2. Bài tập về chuyển động trên mặt phẳng nghiêng: Xác định gia tốc và vận tốc của một vật khi trượt xuống một mặt phẳng nghiêng.
3. Bài tập về hệ vật liên kết bằng dây: Tính toán lực căng trong dây khi hai vật có khối lượng khác nhau được liên kết và chịu tác động của lực ngoài.
4. Bài tập về lực và chuyển động tròn: Xác định lực hướng tâm và gia tốc hướng tâm khi một vật chuyển động tròn đều.

3. Ví Dụ Minh Họa

Ví dụ 1: Một vật có khối lượng 5 kg được kéo trên mặt phẳng ngang với lực 20 N. Hệ số ma sát giữa vật và mặt phẳng là 0.1. Tính gia tốc của vật.

Lời giải:

Lực ma sát được tính bằng:

$$F_{ms} = \mu \cdot N = \mu \cdot m \cdot g$$

Trong đó:

• \(\mu\): Hệ số ma sát
• \(N\): Lực pháp tuyến
• \(m\): Khối lượng của vật
• \(g\): Gia tốc trọng trường (khoảng 9.81 m/s²)

Sau khi tính toán, gia tốc của vật được xác định bằng:

$$a = \frac{F_kéo - F_{ms}}{m}$$

4. Bài Tập Tự Luyện

• Bài tập 1: Một xe có khối lượng 1000 kg chuyển động với gia tốc 2 m/s². Tính lực tác dụng lên xe.
• Bài tập 2: Hai vật có khối lượng lần lượt là 3 kg và 5 kg được nối với nhau bằng một dây không co giãn và kéo bằng lực 24 N. Tính gia tốc của hệ và lực căng trong dây.
• Bài tập 3: Một vật nặng 10 kg được thả rơi tự do từ độ cao 20 m. Bỏ qua lực cản không khí, tính vận tốc của vật khi chạm đất.

5. Kết Luận

Việc thực hành các bài tập nâng cao về định luật 2 Niu-tơn không chỉ giúp học sinh nắm vững kiến thức mà còn phát triển kỹ năng giải quyết vấn đề, tư duy logic và ứng dụng kiến thức vào thực tiễn. Đây là nền tảng quan trọng trong việc học tập và nghiên cứu các lĩnh vực khoa học kỹ thuật.

Định luật 2 Niu-tơn, hay còn gọi là định luật cơ bản của động lực học, được phát biểu bởi nhà khoa học Isaac Newton vào thế kỷ 17. Định luật này là một trong ba định luật cơ bản của cơ học cổ điển, đóng vai trò quan trọng trong việc hiểu và phân tích chuyển động của các vật thể dưới tác động của lực.

Theo định luật này, gia tốc của một vật thể tỉ lệ thuận với tổng các lực tác dụng lên vật thể đó và tỉ lệ nghịch với khối lượng của nó. Công thức toán học biểu diễn định luật 2 Niu-tơn như sau:

$$\vec{F} = m \cdot \vec{a}$$

Trong đó:

• $$\vec{F}$$: Tổng các lực tác dụng lên vật thể (N)
• $$m$$: Khối lượng của vật thể (kg)
• $$\vec{a}$$: Gia tốc của vật thể (m/s²)

Định luật này không chỉ mô tả mối quan hệ giữa lực và chuyển động mà còn là cơ sở để giải quyết các bài toán động lực học. Việc hiểu rõ và áp dụng đúng định luật 2 Niu-tơn giúp chúng ta dự đoán chính xác hành vi của các vật thể trong các tình huống thực tế.

Ví dụ, khi đẩy một chiếc xe với một lực cố định, nếu xe có khối lượng nhỏ, nó sẽ có gia tốc lớn và ngược lại. Điều này minh chứng cho việc gia tốc của vật thể phụ thuộc vào khối lượng và lực tác dụng lên nó, như đã được chỉ ra trong định luật 2 Niu-tơn.

Định luật 2 Niu-tơn cũng là cơ sở để hiểu rõ các khái niệm khác như động lượng, lực hấp dẫn và nhiều hiện tượng vật lý khác trong tự nhiên. Đây là một trong những nền tảng quan trọng trong việc nghiên cứu và ứng dụng khoa học vật lý.

Định luật 2 Niu-tơn không chỉ là một nguyên lý cơ bản trong vật lý mà còn là công cụ quan trọng để giải quyết các bài tập động lực học. Việc áp dụng đúng định luật này giúp chúng ta phân tích và dự đoán chính xác chuyển động của các vật thể trong nhiều tình huống khác nhau. Dưới đây là một số ví dụ về cách áp dụng định luật 2 Niu-tơn trong các bài tập cụ thể.

2.1. Bài Tập Về Lực và Gia Tốc

Để giải các bài tập về lực và gia tốc, chúng ta cần xác định tổng lực tác dụng lên vật thể và khối lượng của nó. Từ đó, ta có thể tính toán gia tốc theo công thức:

$$\vec{a} = \frac{\vec{F}}{m}$$

Ví dụ, nếu một vật thể có khối lượng 5 kg chịu tác dụng của một lực 20 N theo phương ngang, gia tốc của vật thể sẽ được tính như sau:

• $$m = 5 \text{ kg}$$
• $$\vec{F} = 20 \text{ N}$$
• $$\vec{a} = \frac{20}{5} = 4 \text{ m/s}^2$$

2.2. Bài Tập Về Hệ Vật và Dây Nối

Khi giải bài tập về hệ vật và dây nối, ta cần xét tổng lực tác dụng lên toàn bộ hệ thống và áp dụng định luật 2 Niu-tơn cho từng vật trong hệ. Điều này giúp chúng ta tìm ra gia tốc chung và lực căng dây nối giữa các vật.

Ví dụ, xét một hệ gồm hai vật $$m_1$$ và $$m_2$$ nối với nhau bằng một sợi dây không giãn, lực kéo tác dụng lên vật thứ nhất, gia tốc của hệ sẽ là:

$$\vec{a} = \frac{\vec{F}}{m_1 + m_2}$$

2.3. Bài Tập Về Chuyển Động Trên Mặt Phẳng Nghiêng

Trong các bài tập về chuyển động trên mặt phẳng nghiêng, ta cần phân tích lực tác dụng theo hai phương: song song và vuông góc với mặt phẳng nghiêng. Áp dụng định luật 2 Niu-tơn giúp ta tính toán gia tốc của vật thể khi trượt xuống hoặc khi có lực tác dụng ngược chiều.

2.4. Bài Tập Về Lực Ma Sát

Để giải bài tập liên quan đến lực ma sát, ta cần xác định lực ma sát tĩnh hoặc động và tính toán tổng lực tác dụng lên vật thể. Sau đó, áp dụng định luật 2 Niu-tơn để tìm ra gia tốc hoặc lực cần thiết để vật thể bắt đầu chuyển động hoặc giữ nguyên trạng thái chuyển động.

2.5. Bài Tập Về Chuyển Động Tròn

Trong các bài tập về chuyển động tròn, định luật 2 Niu-tơn được áp dụng để tính toán lực hướng tâm cần thiết để duy trì chuyển động tròn đều của vật thể. Lực hướng tâm này được xác định bằng công thức:

$$\vec{F}_{ht} = m \cdot \frac{v^2}{r}$$

Trong đó:

• $$v$$: Vận tốc của vật thể trên quỹ đạo tròn (m/s)
• $$r$$: Bán kính quỹ đạo tròn (m)

Những ví dụ trên cho thấy sự đa dạng trong cách áp dụng định luật 2 Niu-tơn để giải quyết các bài tập khác nhau trong động lực học. Việc luyện tập với nhiều dạng bài tập sẽ giúp học sinh nắm vững hơn về định luật này và cách thức áp dụng nó trong thực tế.

Bài tập liên quan đến định luật 2 Niu-tơn có thể được phân loại dựa trên các tình huống khác nhau trong động lực học. Việc hiểu rõ từng loại bài tập và phương pháp giải sẽ giúp học sinh áp dụng định luật một cách hiệu quả. Dưới đây là một số phân loại phổ biến và phương pháp giải tương ứng:

3.1. Bài Tập Lực và Gia Tốc

Loại bài tập này yêu cầu học sinh tính toán gia tốc của vật thể khi biết lực tác dụng và khối lượng. Phương pháp giải bao gồm:

• Xác định lực tổng hợp tác dụng lên vật thể.
• Tính toán gia tốc bằng cách sử dụng công thức:

  $$\vec{a} = \frac{\vec{F}}{m}$$

• Đối chiếu với điều kiện thực tế của bài toán để suy ra đáp án.

3.2. Bài Tập Hệ Vật và Lực Kéo

Bài tập này thường liên quan đến hệ hai vật kết nối với nhau, như dây nối hay hệ thống ròng rọc. Phương pháp giải:

• Phân tích lực tác dụng lên từng vật.
• Áp dụng định luật 2 Niu-tơn cho từng vật để tìm gia tốc chung của hệ.
• Tính lực căng dây hoặc lực liên kết giữa các vật.

3.3. Bài Tập Chuyển Động Trên Mặt Phẳng Nghiêng

Loại bài tập này liên quan đến việc tính toán chuyển động của vật trên mặt phẳng nghiêng. Phương pháp giải:

• Phân tích các lực tác dụng lên vật, bao gồm trọng lực, lực ma sát và lực pháp tuyến.
• Chia lực trọng trường thành hai thành phần: song song và vuông góc với mặt phẳng nghiêng.
• Áp dụng định luật 2 Niu-tơn cho phương song song để tính gia tốc và các đại lượng liên quan.

3.4. Bài Tập Về Lực Ma Sát

Đối với bài tập liên quan đến lực ma sát, phương pháp giải thường bao gồm:

• Xác định loại lực ma sát (ma sát tĩnh hay động) và tính giá trị của nó.
• Phân tích các lực tác dụng lên vật và tính lực cần thiết để duy trì hoặc làm thay đổi chuyển động.
• Áp dụng định luật 2 Niu-tơn để tìm gia tốc hoặc lực cần thiết.

3.5. Bài Tập Chuyển Động Tròn

Bài tập này yêu cầu tính toán các đại lượng liên quan đến chuyển động tròn như lực hướng tâm, gia tốc hướng tâm. Phương pháp giải:

• Xác định lực hướng tâm cần thiết để duy trì chuyển động tròn, sử dụng công thức:

  $$\vec{F}_{ht} = m \cdot \frac{v^2}{r}$$

• Tính toán các đại lượng như vận tốc, bán kính quỹ đạo và lực tác dụng.

Bằng cách phân loại và áp dụng phương pháp giải thích hợp, học sinh có thể tiếp cận bài tập định luật 2 Niu-tơn một cách dễ dàng và hiệu quả hơn.

Để giúp học sinh củng cố kiến thức và nâng cao kỹ năng giải bài tập, dưới đây là một số bài tập thực hành liên quan đến định luật 2 Niu-tơn. Mỗi bài tập được thiết kế với độ khó khác nhau, phù hợp cho việc ôn luyện từ cơ bản đến nâng cao. Đáp án chi tiết sẽ được cung cấp để học sinh có thể tự đối chiếu và đánh giá kết quả.

Bài Tập 1: Tính Gia Tốc Của Vật

Cho một vật có khối lượng \(m = 5 \, \text{kg}\) chịu tác dụng của lực \(F = 20 \, \text{N}\) theo phương ngang. Bỏ qua mọi lực cản. Hãy tính gia tốc của vật.

• Lời Giải:
• Sử dụng định luật 2 Niu-tơn:

  $$\vec{a} = \frac{\vec{F}}{m} = \frac{20 \, \text{N}}{5 \, \text{kg}} = 4 \, \text{m/s}^2$$

• Vậy gia tốc của vật là \(4 \, \text{m/s}^2\).

Bài Tập 2: Lực Tác Dụng Lên Hệ Vật

Một hệ gồm hai vật có khối lượng \(m_1 = 3 \, \text{kg}\) và \(m_2 = 2 \, \text{kg}\) được nối với nhau bằng một dây nhẹ, không dãn. Hệ thống này chịu tác dụng của một lực kéo \(F = 15 \, \text{N}\) theo phương ngang. Tính gia tốc của hệ và lực căng trong dây.

• Lời Giải:
• Tổng khối lượng của hệ: \(m = m_1 + m_2 = 5 \, \text{kg}\).
• Gia tốc của hệ:

  $$\vec{a} = \frac{\vec{F}}{m} = \frac{15 \, \text{N}}{5 \, \text{kg}} = 3 \, \text{m/s}^2$$

• Lực căng trong dây: \(T = m_2 \times \vec{a} = 2 \, \text{kg} \times 3 \, \text{m/s}^2 = 6 \, \text{N}\).
• Vậy gia tốc của hệ là \(3 \, \text{m/s}^2\) và lực căng trong dây là \(6 \, \text{N}\).

Bài Tập 3: Chuyển Động Trên Mặt Phẳng Nghiêng

Một vật có khối lượng \(m = 10 \, \text{kg}\) trượt không ma sát trên mặt phẳng nghiêng góc \(\theta = 30^\circ\) so với phương ngang. Tính gia tốc của vật.

• Lời Giải:
• Thành phần của lực trọng trường song song với mặt phẳng nghiêng:

  $$F_{song song} = m \cdot g \cdot \sin\theta = 10 \times 9.8 \times \sin 30^\circ = 49 \, \text{N}$$

• Gia tốc của vật:

  $$\vec{a} = \frac{F_{song song}}{m} = \frac{49 \, \text{N}}{10 \, \text{kg}} = 4.9 \, \text{m/s}^2$$

• Vậy gia tốc của vật là \(4.9 \, \text{m/s}^2\).

Bài Tập 4: Lực Ma Sát

Một vật có khối lượng \(m = 8 \, \text{kg}\) trượt trên một mặt phẳng ngang với lực ma sát \(f = 16 \, \text{N}\). Nếu một lực \(F = 40 \, \text{N}\) tác dụng theo phương ngang, hãy tính gia tốc của vật.

• Lời Giải:
• Lực tổng hợp tác dụng lên vật:

  $$F_{tổng} = F - f = 40 \, \text{N} - 16 \, \text{N} = 24 \, \text{N}$$

• Gia tốc của vật:

  $$\vec{a} = \frac{F_{tổng}}{m} = \frac{24 \, \text{N}}{8 \, \text{kg}} = 3 \, \text{m/s}^2$$

• Vậy gia tốc của vật là \(3 \, \text{m/s}^2\).

Các bài tập trên cung cấp một cái nhìn tổng quan về cách áp dụng định luật 2 Niu-tơn trong các tình huống khác nhau, giúp học sinh nắm vững và tự tin hơn khi giải các bài tập nâng cao.

Để nắm vững định luật 2 Niu-tơn và vận dụng nó vào việc giải quyết các bài tập, học sinh cần tham khảo và sử dụng nhiều nguồn tài liệu khác nhau. Dưới đây là một số tài liệu và nguồn học tập hữu ích, bao gồm sách giáo khoa, sách tham khảo, và các trang web học tập trực tuyến.

• Sách giáo khoa và sách tham khảo:
• Sách giáo khoa Vật lý lớp 10: Đây là tài liệu cơ bản giúp học sinh nắm vững lý thuyết về định luật 2 Niu-tơn cũng như các bài tập cơ bản.
• Sách bài tập Vật lý lớp 10: Cung cấp các bài tập từ cơ bản đến nâng cao, giúp học sinh rèn luyện kỹ năng giải bài tập.
• Sách tham khảo "Bài tập Vật lý nâng cao": Dành cho học sinh muốn thử sức với các bài tập phức tạp hơn, giúp nâng cao kỹ năng phân tích và giải quyết vấn đề.
• Các trang web học tập trực tuyến:
• Vật lý 360: Trang web cung cấp các bài giảng video, bài tập trắc nghiệm và tự luận có đáp án chi tiết, giúp học sinh tự học và ôn tập hiệu quả.
• Hocmai.vn: Một nền tảng học tập trực tuyến phổ biến, cung cấp các khóa học về Vật lý, bao gồm cả các bài tập định luật 2 Niu-tơn từ cơ bản đến nâng cao.
• Olm.vn: Trang web này cung cấp các bài tập trắc nghiệm và tự luận được phân loại theo chủ đề, giúp học sinh luyện tập và củng cố kiến thức.
• Phần mềm hỗ trợ học tập:
• Phần mềm Crocodile Physics: Phần mềm mô phỏng Vật lý, cho phép học sinh thực hành và quan sát các hiện tượng vật lý trong môi trường ảo, giúp hiểu rõ hơn về định luật 2 Niu-tơn.
• Ứng dụng "Giải Bài Tập Vật Lý": Ứng dụng di động giúp học sinh tìm kiếm và giải các bài tập Vật lý, bao gồm cả các bài tập nâng cao về định luật 2 Niu-tơn.

Việc sử dụng đa dạng các nguồn tài liệu và công cụ hỗ trợ sẽ giúp học sinh nắm vững kiến thức về định luật 2 Niu-tơn, đồng thời phát triển kỹ năng giải bài tập một cách hiệu quả.