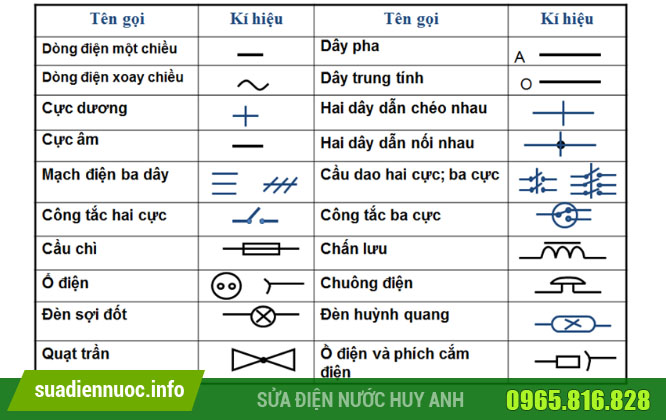
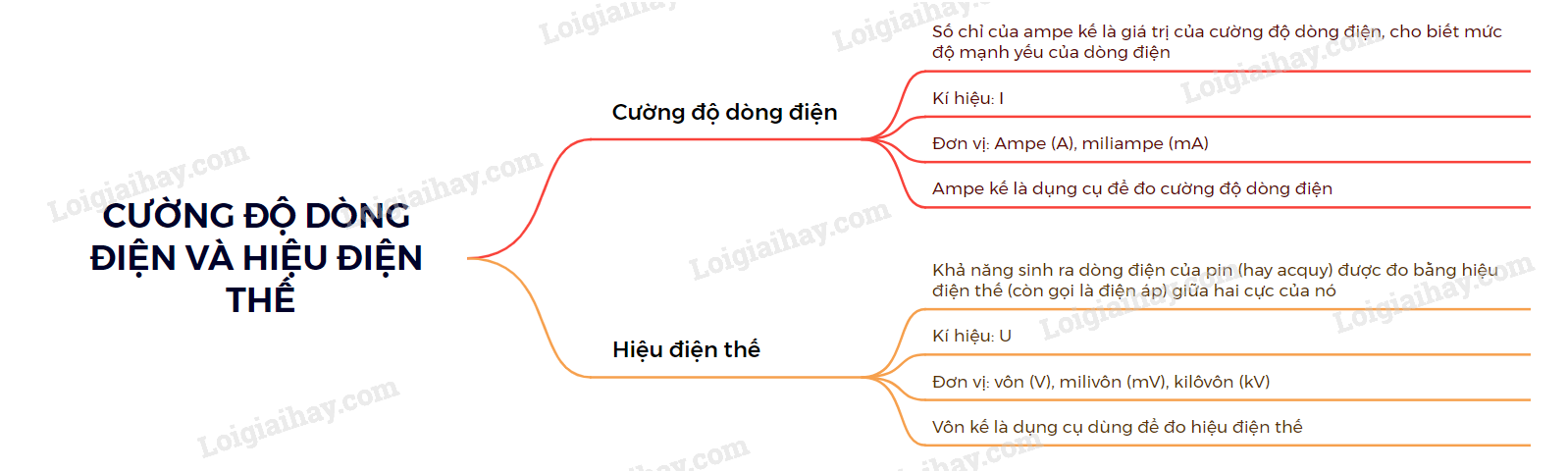
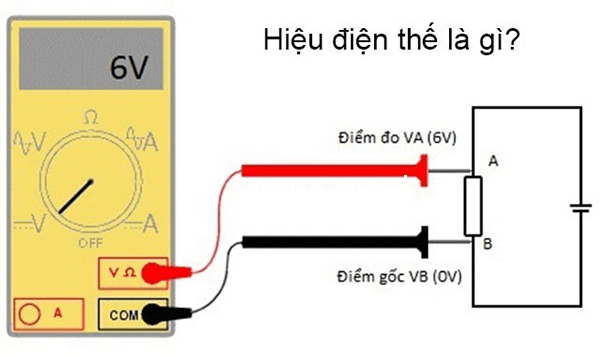
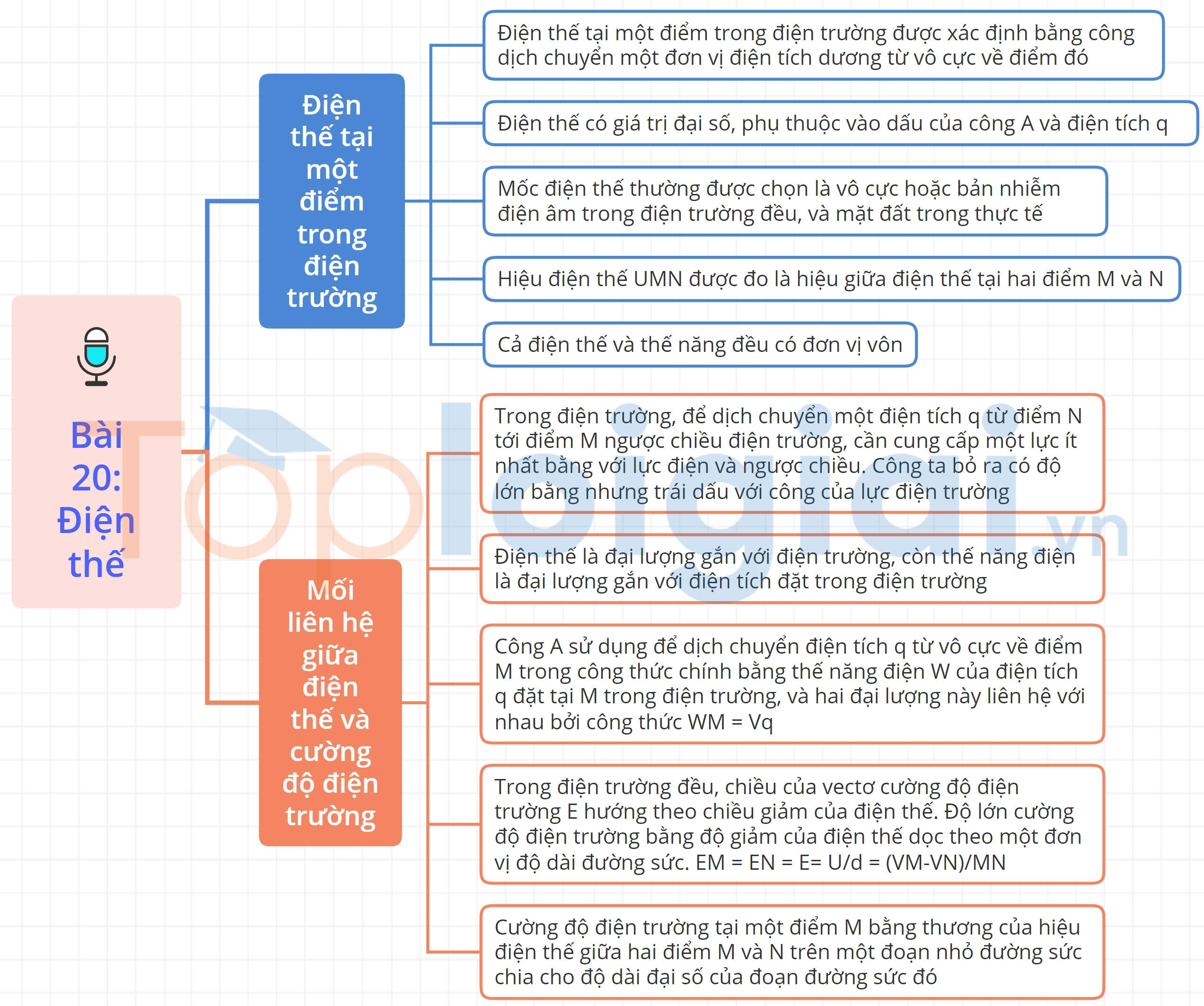
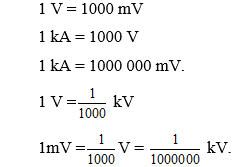Chủ đề bài 20 điện thế: Bài 20: Điện Thế là một khái niệm cơ bản nhưng cực kỳ quan trọng trong Vật lý 11. Bài viết này sẽ giúp bạn nắm vững các kiến thức về điện thế, hiệu điện thế, và cách áp dụng chúng trong các bài tập thực tế. Hãy cùng khám phá để hiểu rõ hơn về thế năng điện và những ứng dụng của nó!
Mục lục
- Bài 20: Điện Thế - Vật Lý 11
- Mục Lục
- Khái Niệm Điện Thế
- Hiệu Điện Thế Giữa Hai Điểm
- Công Thức Liên Hệ Giữa Điện Thế và Cường Độ Điện Trường
- Công Thức Tính Công Dịch Chuyển Trong Điện Trường
- Bài Tập Ứng Dụng Liên Quan Đến Điện Thế
- Mối Liên Hệ Giữa Thế Năng Điện và Điện Thế
- Khái Niệm Điện Thế Trong Điện Trường Đều
- Ứng Dụng Thực Tiễn của Điện Thế
- Khái Niệm Điện Thế
- Hiệu Điện Thế Giữa Hai Điểm
- Công Thức Liên Hệ Giữa Điện Thế và Cường Độ Điện Trường
- Công Thức Tính Công Dịch Chuyển Trong Điện Trường
- Bài Tập Ứng Dụng Liên Quan Đến Điện Thế
- Mối Liên Hệ Giữa Thế Năng Điện và Điện Thế
- Khái Niệm Điện Thế Trong Điện Trường Đều
- Ứng Dụng Thực Tiễn của Điện Thế
Bài 20: Điện Thế - Vật Lý 11
Bài học về Điện Thế là một phần quan trọng trong chương trình Vật lý lớp 11. Nội dung chính của bài học bao gồm khái niệm điện thế, hiệu điện thế, và cách tính công trong điện trường.
I. Khái niệm Điện Thế
Điện thế tại một điểm trong điện trường được xác định bằng công thực hiện để di chuyển một điện tích từ vô cực về điểm đó.
Công thức tính điện thế tại điểm M trong điện trường:
\[ V_M = \frac{A_{M∞}}{q} \]
Trong đó:
- \(V_M\): Điện thế tại điểm \(M\)
- \(A_{M∞}\): Công thực hiện khi di chuyển điện tích \(q\) từ vô cực về điểm \(M\)
- \(q\): Điện tích
II. Hiệu Điện Thế
Hiệu điện thế giữa hai điểm M và N trong điện trường được xác định bằng công thực hiện để di chuyển điện tích từ điểm này đến điểm kia.
Công thức tính hiệu điện thế:
\[ U_{MN} = V_M - V_N \]
Trong đó:
- \(U_{MN}\): Hiệu điện thế giữa hai điểm \(M\) và \(N\)
- \(V_N\): Điện thế tại điểm \(N\)
III. Công Thức Liên Hệ Giữa Điện Thế và Cường Độ Điện Trường
Trong điện trường đều, cường độ điện trường \(E\) và điện thế \(V\) liên hệ với nhau qua công thức:
\[ E = \frac{U_{MN}}{d} \]
Trong đó:
- \(E\): Cường độ điện trường
- \(d\): Khoảng cách giữa hai điểm \(M\) và \(N\)
IV. Bài Tập Ví Dụ
Bài tập: Tính công mà lực điện tác dụng lên một điện tích 5 µC khi nó chuyển động từ điểm \(A\) đến điểm \(B\). Biết \(U_{AB} = 1000 V\).
Giải:
\[ A_{AB} = U_{AB} \cdot q = 1000 \times 5 \times 10^{-6} \, \text{J} = 5 \, \text{mJ} \]
V. Luyện Tập
Sau khi học xong bài này, học sinh cần nắm vững các kiến thức sau:
- Giải thích được ý nghĩa của hiệu điện thế giữa hai điểm.
- Vận dụng mối liên hệ giữa thế năng điện và điện thế để tính toán.
- Biết cách tính công dịch chuyển của điện tích trong điện trường.

.png)
Mục Lục
I. Giới Thiệu Về Điện Thế
1.1 Khái niệm Điện Thế
1.2 Thế Năng Điện và Điện Thế
II. Hiệu Điện Thế
2.1 Định nghĩa Hiệu Điện Thế
2.2 Công thức tính Hiệu Điện Thế
2.3 Ứng dụng thực tế của Hiệu Điện Thế
III. Điện Trường và Điện Thế
3.1 Mối quan hệ giữa Điện Trường và Điện Thế
3.2 Công thức liên hệ: \[ E = \frac{U_{MN}}{d} \]
3.3 Ví dụ minh họa
IV. Bài Tập Về Điện Thế
4.1 Bài tập tính toán Điện Thế
4.2 Bài tập về Hiệu Điện Thế
4.3 Bài tập liên quan đến công dịch chuyển
V. Ứng Dụng Của Điện Thế Trong Đời Sống
5.1 Ứng dụng trong kỹ thuật điện
5.2 Ứng dụng trong điện tử
Khái Niệm Điện Thế
Điện thế là một đại lượng vật lý đặc trưng cho mức độ mạnh yếu của điện trường tại một điểm, thể hiện qua khả năng thực hiện công của điện trường. Điện thế tại một điểm M trong điện trường được xác định bằng công thực hiện để di chuyển một đơn vị điện tích dương từ vô cực đến điểm M mà không cần thay đổi động năng.
Điện Thế Tại Một Điểm
Điện thế \(V_M\) tại một điểm M trong điện trường được tính bằng công \(A\) cần để dịch chuyển một đơn vị điện tích thử \(q\) từ vô cực về điểm đó:
\[ V_M = \frac{A}{q} \]
Trong đó:
- \(V_M\) là điện thế tại điểm M.
- \(A\) là công thực hiện bởi lực điện.
- \(q\) là điện tích thử dương.
Đơn Vị Đo Điện Thế
Đơn vị đo điện thế là vôn (V). Một vôn tương ứng với công 1 jun (J) thực hiện để dịch chuyển một điện tích 1 culông (C) từ một điểm này đến điểm khác trong điện trường.

Hiệu Điện Thế Giữa Hai Điểm
Hiệu điện thế giữa hai điểm trong một điện trường là đại lượng đặc trưng cho khả năng sinh công của điện trường trong quá trình dịch chuyển một điện tích thử từ điểm này đến điểm kia. Hiệu điện thế này là sự chênh lệch về điện thế giữa hai điểm và có thể hiểu đơn giản là năng lượng cần thiết để di chuyển một đơn vị điện tích qua điện trường.
Định Nghĩa Hiệu Điện Thế
Hiệu điện thế giữa hai điểm \( M \) và \( N \) được định nghĩa là:
\[
U_{MN} = V_M - V_N = \frac{A_{MN}}{q}
\]
Trong đó:
- \( U_{MN} \) là hiệu điện thế giữa hai điểm \( M \) và \( N \), đơn vị đo là Vôn (V).
- \( V_M \) và \( V_N \) là điện thế tại các điểm \( M \) và \( N \).
- \( A_{MN} \) là công của lực điện khi di chuyển điện tích thử từ \( M \) đến \( N \), đơn vị đo là Joule (J).
- \( q \) là độ lớn của điện tích thử, đơn vị đo là Coulomb (C).
Công Thức Liên Quan
Nếu biết cường độ điện trường \( E \) và khoảng cách \( d \) giữa hai điểm trong điện trường đều, hiệu điện thế có thể tính bằng công thức:
\[
U = E \cdot d
\]
Ví Dụ Minh Họa
Giả sử có một điện tích thử \( q = 2 \, \text{C} \) di chuyển từ điểm \( M \) với điện thế \( V_M = 10 \, \text{V} \) đến điểm \( N \) với điện thế \( V_N = 4 \, \text{V} \). Hiệu điện thế giữa hai điểm này là:
\[
U_{MN} = V_M - V_N = 10 \, \text{V} - 4 \, \text{V} = 6 \, \text{V}
\]
Như vậy, hiệu điện thế giữa \( M \) và \( N \) là \( 6 \, \text{V} \).
Công Thức Liên Hệ Giữa Điện Thế và Cường Độ Điện Trường
Trong điện trường đều, mối liên hệ giữa điện thế và cường độ điện trường được thể hiện qua một công thức cơ bản, giúp chúng ta hiểu rõ hơn về mối quan hệ này:
- Cường độ điện trường \( E \) và hiệu điện thế \( U \) giữa hai điểm trong điện trường đều có mối quan hệ với khoảng cách \( d \) giữa hai điểm đó. Công thức thể hiện mối liên hệ này là:
\[
U = E \cdot d
\]
Trong đó:
- \( U \) là hiệu điện thế giữa hai điểm (đơn vị: Vôn - V).
- \( E \) là cường độ điện trường (đơn vị: Vôn trên mét - V/m).
- \( d \) là khoảng cách giữa hai điểm (đơn vị: mét - m).
Điều này cho thấy, trong một điện trường đều, hiệu điện thế giữa hai điểm tỉ lệ thuận với cường độ điện trường và khoảng cách giữa chúng. Cường độ điện trường càng lớn hoặc khoảng cách giữa hai điểm càng xa, thì hiệu điện thế giữa chúng cũng càng lớn.
Ví dụ: Nếu cường độ điện trường là \( 500 \, V/m \) và khoảng cách giữa hai điểm là \( 2 \, m \), thì hiệu điện thế giữa hai điểm này sẽ là:
\[
U = 500 \cdot 2 = 1000 \, V
\]
Qua công thức trên, chúng ta có thể dễ dàng tính toán và áp dụng trong các bài tập liên quan đến điện thế và cường độ điện trường.

Công Thức Tính Công Dịch Chuyển Trong Điện Trường
Công của lực điện khi dịch chuyển một điện tích trong điện trường là một khái niệm cơ bản trong Vật lý 11. Để tính công của lực điện, chúng ta sử dụng công thức sau:
\[
A = q \cdot E \cdot d
\]
Trong đó:
- \( A \) là công của lực điện (đơn vị: Joule - J)
- \( q \) là điện tích dịch chuyển (đơn vị: Coulomb - C)
- \( E \) là cường độ điện trường (đơn vị: V/m)
- \( d \) là khoảng cách dịch chuyển theo phương của điện trường (đơn vị: mét - m)
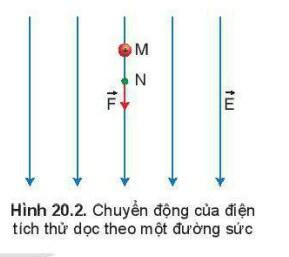
Trong trường hợp điện trường đều, công của lực điện chỉ phụ thuộc vào vị trí của điểm đầu và điểm cuối của đường dịch chuyển, không phụ thuộc vào hình dạng đường đi. Khi điện tích dịch chuyển dọc theo một đường sức trong điện trường đều, công được xác định dựa trên khoảng cách \( d \) giữa hai điểm theo phương của đường sức.
Nếu điện tích dịch chuyển cùng chiều với điện trường, công của lực điện sẽ dương (\( A > 0 \)). Ngược lại, nếu điện tích dịch chuyển ngược chiều với điện trường, công của lực điện sẽ âm (\( A < 0 \)). Công thức này có thể áp dụng cho nhiều bài tập tính toán và lý thuyết liên quan đến lực điện trong điện trường đều.
XEM THÊM:
Bài Tập Ứng Dụng Liên Quan Đến Điện Thế
Bài tập về điện thế là một phần quan trọng trong chương trình Vật lý 11, giúp củng cố kiến thức và áp dụng lý thuyết vào thực tế. Dưới đây là một số bài tập minh họa:
Bài Tập 1: Tính Công Của Điện Trường
Cho một điện tích \( q = 2 \times 10^{-6} \, C \) dịch chuyển từ điểm M đến điểm N trong một điện trường. Biết hiệu điện thế giữa hai điểm là \( U_{MN} = 100 \, V \). Tính công của điện trường khi dịch chuyển điện tích này.
- Lời giải:
- Công của điện trường được tính theo công thức: \( A = U_{MN} \cdot q \)
- Thay các giá trị vào: \( A = 100 \, V \cdot 2 \times 10^{-6} \, C = 2 \times 10^{-4} \, J \)
Bài Tập 2: Hiệu Điện Thế Trong Điện Trường Đều
Một điện trường đều có cường độ \( E = 5000 \, V/m \). Một điện tích \( q = 3 \times 10^{-9} \, C \) được đặt trong điện trường này. Tính hiệu điện thế giữa hai điểm cách nhau 10 cm theo hướng song song với đường sức điện.
- Lời giải:
- Hiệu điện thế được tính theo công thức: \( U = E \cdot d \)
- Với \( d = 0.1 \, m \), ta có: \( U = 5000 \cdot 0.1 = 500 \, V \)
Bài Tập 3: Bài Toán Tam Giác Trong Điện Trường
Trong một tam giác vuông đặt trong điện trường đều, biết cạnh BC = 6 cm và \( U_{BC} = 120 \, V \). Hãy tính hiệu điện thế giữa hai điểm A và B, và cường độ điện trường \( E_0 \).
- Lời giải:
- Ta có: \( U_{AC} = 0 \, V \) vì góc giữa \( AC \) và đường sức là 90°.
- Tính \( E_0 \) từ \( U_{BC} = E_0 \cdot BC \cdot \cos 60^\circ \): \( E_0 = \frac{120}{0.06 \cdot 0.5} = 4000 \, V/m \)
Bài Tập 4: Điện Thế Tại Một Điểm Trong Điện Trường Đều
Cho điện trường đều có cường độ \( E = 2000 \, V/m \). Một điểm nằm cách nguồn điện 15 cm. Tính điện thế tại điểm đó.
- Lời giải:
- Điện thế tại một điểm được tính bằng công thức: \( V = E \cdot d \)
- Với \( d = 0.15 \, m \), ta có: \( V = 2000 \cdot 0.15 = 300 \, V \)
Kết Luận
Những bài tập trên không chỉ giúp học sinh nắm vững công thức mà còn biết cách áp dụng chúng vào các tình huống thực tế. Thực hành thường xuyên là chìa khóa để làm chủ kiến thức về điện thế.

Mối Liên Hệ Giữa Thế Năng Điện và Điện Thế
Mối liên hệ giữa thế năng điện và điện thế là một trong những khái niệm cơ bản trong vật lý điện trường. Để hiểu rõ hơn, chúng ta cần xem xét hai đại lượng này:
- Thế năng điện (\( W \)): Là năng lượng của một điện tích khi nó nằm trong một điện trường. Thế năng này phụ thuộc vào vị trí của điện tích trong điện trường và giá trị của điện tích đó. Công thức xác định thế năng điện của một điện tích \( q \) tại điểm M là:
\[
W = V \cdot q
\]
Trong đó:
- \( W \) là thế năng điện (Joule).
- \( V \) là điện thế tại điểm M (Volt).
- \( q \) là điện tích (Coulomb).
- Điện thế (\( V \)): Điện thế tại một điểm trong điện trường đặc trưng cho mức năng lượng mà điện tích sẽ có khi nằm tại điểm đó. Điện thế được tính dựa trên công cần thiết để dịch chuyển một điện tích dương từ vô cực về điểm đó.
Từ công thức trên, ta thấy rằng điện thế là đại lượng đặc trưng cho điểm trong điện trường, trong khi thế năng là đại lượng gắn liền với điện tích cụ thể tại điểm đó. Mối liên hệ giữa chúng được thể hiện qua công thức:
Điều này có nghĩa là, khi biết thế năng và điện tích tại một điểm, ta có thể xác định được điện thế tại điểm đó, và ngược lại. Điện thế và thế năng đều là những khái niệm quan trọng để hiểu rõ hơn về hành vi của các điện tích trong một điện trường.

Khái Niệm Điện Thế Trong Điện Trường Đều
Điện trường đều là điện trường mà các đường sức điện song song và cách đều nhau. Một ví dụ điển hình là điện trường giữa hai bản kim loại phẳng song song mang điện tích trái dấu.
Trong điện trường đều, điện thế tại một điểm M được xác định bằng công thức:
\[
V_M = - E \cdot d
\]
Trong đó:
- E: Cường độ điện trường (V/m).
- d: Khoảng cách từ điểm M đến điểm gốc.
Vì điện trường đều nên cường độ điện trường \( E \) có giá trị không đổi. Điện thế V tại một điểm trong điện trường đều có quan hệ trực tiếp với cường độ điện trường và khoảng cách từ điểm đó đến gốc. Đặc biệt, điện thế giảm dần khi ta đi theo chiều của cường độ điện trường.
Điều này có nghĩa là, trong một điện trường đều, nếu ta di chuyển ngược chiều với chiều của đường sức điện, điện thế sẽ tăng lên. Điện thế tại bất kỳ điểm nào trên một mặt phẳng vuông góc với các đường sức điện đều như nhau.
Ứng Dụng Thực Tiễn của Điện Thế
Điện thế là một đại lượng vật lý quan trọng với nhiều ứng dụng thực tiễn trong đời sống và công nghiệp. Dưới đây là một số ứng dụng tiêu biểu:
- Hệ thống điện gia dụng: Điện thế và hiệu điện thế được sử dụng trong các thiết bị điện như tivi, tủ lạnh, máy giặt để đảm bảo hoạt động ổn định và an toàn.
- Truyền tải điện: Trong hệ thống truyền tải điện, hiệu điện thế cao giúp giảm tổn thất điện năng khi truyền tải từ nhà máy điện đến khu dân cư.
- Công nghiệp sản xuất: Các nhà máy sử dụng điện thế và hiệu điện thế được kiểm soát chặt chẽ để đảm bảo hiệu quả và độ bền của máy móc.
- Thiết bị điện tử: Điện thế cần thiết cho các linh kiện điện tử như vi xử lý, mạch tích hợp, và tụ điện để hoạt động chính xác.
- Năng lượng tái tạo: Hệ thống năng lượng mặt trời và gió sử dụng điện thế để chuyển đổi và lưu trữ điện năng hiệu quả.
Nhờ những ứng dụng này, điện thế đóng vai trò quan trọng trong việc duy trì và phát triển các công nghệ hiện đại, từ các thiết bị gia dụng thông thường đến các hệ thống phức tạp trong công nghiệp và năng lượng.

Khái Niệm Điện Thế
Điện thế tại một điểm trong điện trường là một đại lượng vật lý dùng để xác định mức độ ảnh hưởng của điện trường lên điện tích tại điểm đó. Điện thế được định nghĩa là đại lượng đặc trưng cho khả năng sinh công của điện trường tại một điểm, khi có một điện tích thử được đặt tại điểm đó.
Điện thế tại một điểm M trong điện trường được xác định bởi công thức:
\[ V_M = \frac{A}{q} \]
Trong đó:
- \( V_M \): Điện thế tại điểm M.
- \( A \): Công của lực điện thực hiện khi di chuyển điện tích thử \( q \) từ vô cực đến điểm M.
- \( q \): Điện tích thử dương.
Điện thế có đơn vị là Vôn (V). Đối với điện trường đều, điện thế tại các điểm trên cùng một mặt đẳng thế là như nhau. Điện thế thường được sử dụng để tính hiệu điện thế giữa hai điểm và để phân tích sự di chuyển của điện tích trong các mạch điện.
Mốc điện thế thường được chọn là vô cực hoặc mặt đất, nơi có điện thế bằng 0. Điều này giúp ta dễ dàng so sánh điện thế giữa các điểm khác nhau trong không gian hoặc trong mạch điện.
Hiệu Điện Thế Giữa Hai Điểm
Hiệu điện thế giữa hai điểm trong điện trường là đại lượng đặc trưng cho khả năng sinh công của lực điện trong việc di chuyển điện tích từ điểm này đến điểm khác. Hiệu điện thế giữa hai điểm \( M \) và \( N \) được tính bằng hiệu của điện thế tại hai điểm đó:
Trong đó:
- \( U_{MN} \) là hiệu điện thế giữa hai điểm \( M \) và \( N \) (đơn vị: Vôn - V).
- \( V_M \) và \( V_N \) lần lượt là điện thế tại điểm \( M \) và \( N \).
Hiệu điện thế có thể được đo bằng các thiết bị như tĩnh điện kế, và nó thể hiện sự chênh lệch về thế năng mà một điện tích \( q \) trải qua khi di chuyển giữa hai điểm trong điện trường. Điều này có nghĩa là nếu \( U_{MN} \) lớn, lực điện trường tác dụng lên điện tích để di chuyển từ \( M \) đến \( N \) sẽ thực hiện một công lớn hơn.
Nếu xét trong một điện trường đều, công thức tính hiệu điện thế có thể được liên hệ với cường độ điện trường \( E \) và khoảng cách \( d \) giữa hai điểm theo công thức:
Trong công thức trên:
- \( E \) là cường độ điện trường (đơn vị: V/m).
- \( d \) là khoảng cách giữa hai điểm theo phương của điện trường (đơn vị: m).
Công thức này cho thấy, trong điện trường đều, hiệu điện thế giữa hai điểm tỉ lệ thuận với cường độ điện trường và khoảng cách giữa chúng.
Công Thức Liên Hệ Giữa Điện Thế và Cường Độ Điện Trường
Trong vật lý, cường độ điện trường \( E \) và điện thế \( V \) tại một điểm trong điện trường có mối liên hệ chặt chẽ với nhau. Mối liên hệ này giúp chúng ta hiểu rõ hơn về cách điện thế thay đổi theo vị trí trong điện trường, đặc biệt là trong điện trường đều.
Nếu xét trong một điện trường đều, mối liên hệ giữa cường độ điện trường \( E \) và sự thay đổi của điện thế \( \Delta V \) dọc theo một đoạn thẳng \( d \) trong điện trường được biểu diễn bằng công thức:
Trong đó:
- \( E \) là cường độ điện trường (đơn vị: V/m).
- \( \Delta V \) là độ biến thiên điện thế giữa hai điểm (đơn vị: V).
- \( d \) là khoảng cách giữa hai điểm theo phương của điện trường (đơn vị: m).
Dấu âm trong công thức biểu thị rằng cường độ điện trường có hướng từ điểm có điện thế cao đến điểm có điện thế thấp, tức là cùng hướng với sự giảm của điện thế. Điều này có nghĩa là nếu bạn biết cường độ điện trường và khoảng cách giữa hai điểm, bạn có thể dễ dàng tính được sự thay đổi của điện thế giữa hai điểm đó và ngược lại.
Trong trường hợp điện trường không đều, công thức tổng quát hơn để tính cường độ điện trường tại một điểm \( M \) được cho bởi:
Ở đây, \( \frac{dV}{dx} \) là đạo hàm của điện thế theo khoảng cách, biểu diễn sự thay đổi của điện thế khi di chuyển dọc theo một đường sức trong điện trường.
Các công thức trên là nền tảng quan trọng trong việc phân tích và giải quyết các bài toán liên quan đến điện thế và cường độ điện trường trong vật lý.

Công Thức Tính Công Dịch Chuyển Trong Điện Trường
Trong một điện trường, công của lực điện trường dịch chuyển một điện tích \( q \) từ điểm \( M \) đến điểm \( N \) được xác định bằng công thức:
Trong đó:
- \( A \): Công của lực điện trường (Joule - J).
- \( q \): Điện tích dịch chuyển (Coulomb - C).
- \( E \): Cường độ điện trường (Vôn trên mét - V/m).
- \( d \): Khoảng cách giữa điểm đầu và điểm cuối, tính theo chiều của vectơ cường độ điện trường (mét - m).
Các lưu ý khi sử dụng công thức này:
- Nếu điện tích di chuyển cùng chiều với vectơ cường độ điện trường, thì \( d > 0 \) và \( A \) sẽ có giá trị dương, biểu thị công được sinh ra.
- Nếu điện tích di chuyển ngược chiều với vectơ cường độ điện trường, thì \( d < 0 \) và \( A \) sẽ có giá trị âm, biểu thị công được tiêu tốn.
- Nếu điện tích di chuyển theo đường cong khép kín trong điện trường đều, tổng công \( A \) sẽ bằng 0 do điểm đầu và điểm cuối trùng nhau.
Ví dụ minh họa:
Giả sử một điện tích \( q = 2 \, \mu C \) (micro-Coulomb) di chuyển ngược chiều với một đường sức trong một điện trường đều \( E = 1000 \, V/m \) trên quãng đường dài \( d = 1 \, m \). Công của lực điện trường được tính như sau:
Như vậy, công của lực điện trong trường hợp này là \( -2 \, mJ \), nghĩa là công tiêu tốn để dịch chuyển điện tích.
Bài Tập Ứng Dụng Liên Quan Đến Điện Thế
Trong phần này, chúng ta sẽ giải quyết một số bài tập liên quan đến điện thế và hiệu điện thế nhằm củng cố kiến thức đã học và áp dụng vào thực tế.
Bài Tập 1: Xác Định Điện Thế Tại Các Điểm Trong Mạch Điện
- Đề bài: Cho một mạch điện gồm nguồn điện 12V và hai điện trở mắc nối tiếp với các giá trị lần lượt là \(R_1 = 2Ω\) và \(R_2 = 4Ω\). Hãy tính điện thế tại điểm nối giữa hai điện trở.
- Giải:
- Tính tổng trở của mạch: \[R_{tổng} = R_1 + R_2 = 2Ω + 4Ω = 6Ω\]
- Tính dòng điện trong mạch: \[I = \frac{V}{R_{tổng}} = \frac{12V}{6Ω} = 2A\]
- Điện thế tại điểm nối giữa \(R_1\) và \(R_2\): \[V = IR_1 = 2A \times 2Ω = 4V\]
Bài Tập 2: Tính Hiệu Điện Thế Giữa Hai Điểm Trong Mạch Điện
- Đề bài: Cho một mạch điện gồm nguồn điện 9V và hai điện trở mắc nối tiếp với các giá trị \(R_1 = 3Ω\) và \(R_2 = 6Ω\). Tính hiệu điện thế giữa hai đầu điện trở \(R_1\).
- Giải:
- Tổng trở của mạch: \[R_{tổng} = R_1 + R_2 = 3Ω + 6Ω = 9Ω\]
- Dòng điện trong mạch: \[I = \frac{V}{R_{tổng}} = \frac{9V}{9Ω} = 1A\]
- Hiệu điện thế giữa hai đầu điện trở \(R_1\): \[U = IR_1 = 1A \times 3Ω = 3V\]
Bài Tập 3: Ứng Dụng Thực Tiễn Của Hiệu Điện Thế
- Đề bài: Một máy biến áp sử dụng hiệu điện thế 220V để cung cấp điện cho một thiết bị yêu cầu 110V. Tính hiệu điện thế giữa các đầu của máy biến áp và cho biết hiệu điện thế này sẽ ảnh hưởng như thế nào đến hoạt động của thiết bị.
- Giải:
Máy biến áp cần giảm hiệu điện thế từ 220V xuống 110V để phù hợp với yêu cầu của thiết bị. Nếu hiệu điện thế này được điều chỉnh đúng, thiết bị sẽ hoạt động bình thường và an toàn. Ngược lại, nếu hiệu điện thế không được điều chỉnh đúng cách, có thể dẫn đến hỏng hóc hoặc hoạt động không ổn định của thiết bị.
Mối Liên Hệ Giữa Thế Năng Điện và Điện Thế
Mối quan hệ giữa thế năng điện và điện thế là một trong những khái niệm cơ bản trong vật lý điện. Thế năng điện \( W \) tại một điểm trong điện trường được xác định bởi công cần thiết để dịch chuyển một điện tích từ một điểm tham chiếu (thường là vô cực) đến điểm đó trong điện trường.
Điện thế \( V \) tại một điểm là đại lượng đo bằng thương số của thế năng điện \( W \) và điện tích \( q \) tại điểm đó:
\[
V = \frac{W}{q}
\]
Điều này có nghĩa là điện thế đặc trưng cho khả năng thực hiện công của điện trường lên một đơn vị điện tích. Nếu biết được điện thế \( V \) và điện tích \( q \), chúng ta có thể tính được thế năng điện bằng cách nhân điện thế với điện tích:
\[
W = V \cdot q
\]
Trong trường hợp điện trường đều, mối quan hệ giữa điện thế và cường độ điện trường \( E \) cũng có thể được biểu diễn qua công thức:
\[
E = - \frac{\Delta V}{\Delta s}
\]
Trong đó:
- \( E \) là cường độ điện trường.
- \( \Delta V \) là sự thay đổi điện thế giữa hai điểm.
- \( \Delta s \) là khoảng cách giữa hai điểm trong điện trường.
Với mối liên hệ này, chúng ta có thể thấy rằng cường độ điện trường lớn hơn khi sự thay đổi điện thế trên một khoảng cách nhất định là lớn hơn.
Để hiểu rõ hơn, hãy xem xét một ví dụ cụ thể: Nếu một điện tích dương được dịch chuyển trong điện trường từ điểm A có điện thế \( V_A \) đến điểm B có điện thế \( V_B \), công của lực điện trường thực hiện lên điện tích đó được tính bằng:
\[
A_{AB} = q \cdot (V_A - V_B)
\]
Qua công thức này, chúng ta thấy rằng nếu \( V_A > V_B \), thì công sẽ có giá trị dương, nghĩa là điện trường sinh công khi dịch chuyển điện tích. Ngược lại, nếu \( V_A < V_B \), công sẽ có giá trị âm, nghĩa là cần phải cung cấp công để dịch chuyển điện tích.
Khái Niệm Điện Thế Trong Điện Trường Đều
Điện thế trong một điện trường đều là một khái niệm quan trọng trong vật lý, đặc biệt khi nghiên cứu về tương tác giữa các điện tích. Điện trường đều là loại điện trường có cường độ điện trường E không đổi tại mọi điểm. Điều này dẫn đến một số đặc điểm đặc trưng cho điện thế trong loại điện trường này.
Trong điện trường đều, sự thay đổi điện thế giữa hai điểm được xác định bởi công thức:
\[ \Delta V = -E \cdot d \cdot \cos\theta \]
Trong đó:
- E là cường độ điện trường, có đơn vị là V/m.
- d là khoảng cách giữa hai điểm trong điện trường.
- \(\theta\) là góc giữa phương của cường độ điện trường và đường thẳng nối giữa hai điểm.
Đặc biệt, nếu xét trường hợp \(\theta = 0^\circ\) (điện trường cùng phương với đường nối hai điểm), công thức trên trở thành:
\[ \Delta V = -E \cdot d \]
Điều này có nghĩa là điện thế sẽ giảm dần theo hướng của điện trường, và độ lớn của sự giảm điện thế tỉ lệ thuận với cường độ điện trường và khoảng cách giữa hai điểm.
Ví dụ minh họa: Giả sử ta có một điện trường đều với cường độ E = 1000 V/m, và xét hai điểm A và B cách nhau 2m theo phương của điện trường. Khi đó, sự chênh lệch điện thế giữa hai điểm A và B được tính là:
\[ \Delta V_{AB} = -1000 \cdot 2 = -2000 \text{ V} \]
Điều này có nghĩa là điện thế tại điểm B thấp hơn tại điểm A 2000 V.
Ứng Dụng Thực Tiễn của Điện Thế
Điện thế có nhiều ứng dụng thực tiễn trong đời sống hàng ngày cũng như trong các lĩnh vực công nghiệp và công nghệ. Các ứng dụng này không chỉ giúp đảm bảo an toàn và hiệu quả trong việc sử dụng các thiết bị điện mà còn góp phần quan trọng trong quá trình sản xuất và truyền tải điện năng.
- Hệ thống điện gia dụng: Điện thế và hiệu điện thế được sử dụng để vận hành các thiết bị như tivi, tủ lạnh, máy giặt, giúp chúng hoạt động ổn định và an toàn. Điện thế trong các hệ thống gia dụng thường là 220V.
- Truyền tải điện năng: Hiệu điện thế cao (110kV - 500kV) được sử dụng trong quá trình truyền tải điện năng từ các nhà máy điện đến các khu dân cư và khu công nghiệp. Việc này giúp giảm thiểu tổn thất điện năng trên đường dây truyền tải dài.
- Công nghiệp sản xuất: Trong các nhà máy, điện thế và hiệu điện thế được điều chỉnh để các máy móc hoạt động với hiệu suất tối ưu. Điện thế sử dụng trong công nghiệp thường dao động từ 220V đến 380V.
- Thiết bị điện tử: Điện thế đóng vai trò quan trọng trong việc vận hành các linh kiện điện tử như vi xử lý, mạch tích hợp, và tụ điện. Mức điện thế phổ biến trong lĩnh vực này là từ 5V đến 12V.
- Năng lượng tái tạo: Các hệ thống như năng lượng mặt trời và gió sử dụng hiệu điện thế để chuyển đổi và lưu trữ điện năng. Thông thường, các hệ thống này hoạt động với mức điện thế từ 12V đến 48V.
Như vậy, điện thế và hiệu điện thế không chỉ là các khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày, từ việc đảm bảo hoạt động của các thiết bị điện trong gia đình đến việc truyền tải và sử dụng năng lượng trong công nghiệp và năng lượng tái tạo.