Chủ đề 1 nhiệt lượng kế chứa 2 lít nước: Khám phá cách giải bài toán liên quan đến "1 nhiệt lượng kế chứa 2 lít nước" với các phương pháp tính toán chính xác và ứng dụng thực tế trong đời sống. Bài viết này sẽ giúp bạn nắm vững kiến thức nhiệt học và cách áp dụng nguyên lý cân bằng nhiệt một cách hiệu quả nhất.
Mục lục
Tổng hợp thông tin về "1 nhiệt lượng kế chứa 2 lít nước"
Từ khóa "1 nhiệt lượng kế chứa 2 lít nước" thường xuất hiện trong các bài tập vật lý, đặc biệt liên quan đến chủ đề nhiệt học. Các bài toán này thường yêu cầu tính toán sự thay đổi nhiệt độ của nước khi một vật nóng được đặt vào nhiệt lượng kế. Dưới đây là tổng hợp chi tiết về thông tin thu thập được từ kết quả tìm kiếm:
1. Nội dung bài toán
Bài toán thường đề cập đến việc:
- Một nhiệt lượng kế chứa 2 lít nước ở nhiệt độ ban đầu, ví dụ như
\(15^\circ C\) . - Bỏ vào nhiệt lượng kế một quả cầu bằng đồng thau hoặc một kim loại khác đã được nung nóng đến một nhiệt độ cao, ví dụ như
\(100^\circ C\) . - Nhiệm vụ là tính nhiệt độ cuối cùng của nước khi đạt cân bằng nhiệt, thường sử dụng công thức cân bằng nhiệt
\(Q_{\text{thu}} = Q_{\text{tỏa}}\) .
2. Các bước giải quyết bài toán
Các bài toán này thường được giải theo các bước sau:
- Xác định nhiệt lượng do quả cầu tỏa ra:
Q_{tỏa} = m_1 \cdot c_1 \cdot \Delta t_1 , trong đó\(m_1\) là khối lượng quả cầu,\(c_1\) là nhiệt dung riêng của quả cầu, và\(\Delta t_1\) là sự thay đổi nhiệt độ của quả cầu. - Xác định nhiệt lượng nước thu vào:
Q_{thu} = m_2 \cdot c_2 \cdot \Delta t_2 , trong đó\(m_2\) là khối lượng nước,\(c_2\) là nhiệt dung riêng của nước, và\(\Delta t_2\) là sự thay đổi nhiệt độ của nước. - Thiết lập phương trình cân bằng nhiệt:
Q_{thu} = Q_{tỏa} . - Giải phương trình để tìm nhiệt độ cuối cùng
t .
3. Ví dụ cụ thể
Một ví dụ cụ thể của bài toán:
- Nước: khối lượng
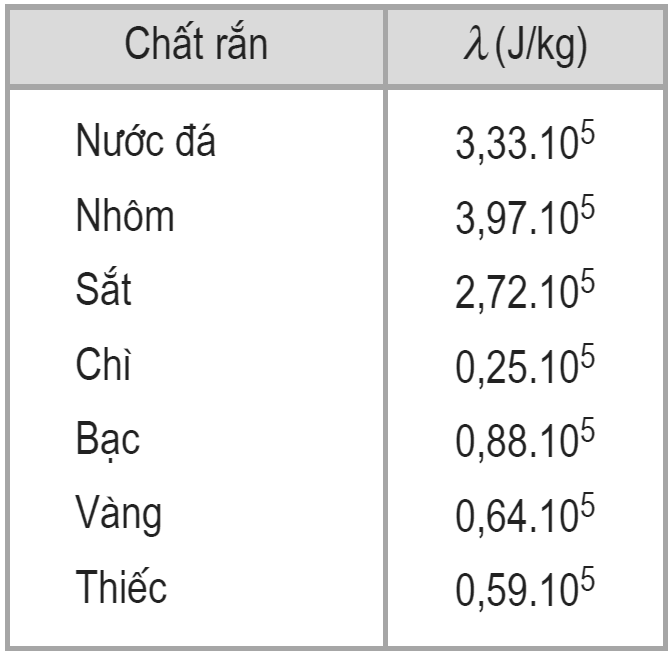
\(2 \, kg\) , nhiệt dung riêng\(4186 \, J/kg.K\) , nhiệt độ ban đầu\(15^\circ C\) . - Quả cầu đồng: khối lượng
\(0,5 \, kg\) , nhiệt dung riêng\(368 \, J/kg.K\) , nhiệt độ ban đầu\(100^\circ C\) . - Thiết lập và giải phương trình
0,5 \cdot 368 \cdot (100 - t) = 2 \cdot 4186 \cdot (t - 15) , tìm đượct ≈ 16,83^\circ C .
4. Ý nghĩa giáo dục
Các bài toán dạng này giúp học sinh hiểu rõ hơn về nguyên lý bảo toàn năng lượng trong hệ kín, cũng như cách áp dụng các công thức vật lý vào việc giải quyết các tình huống thực tế. Đây là một dạng bài tập quan trọng trong chương trình học Vật lý ở cấp trung học.
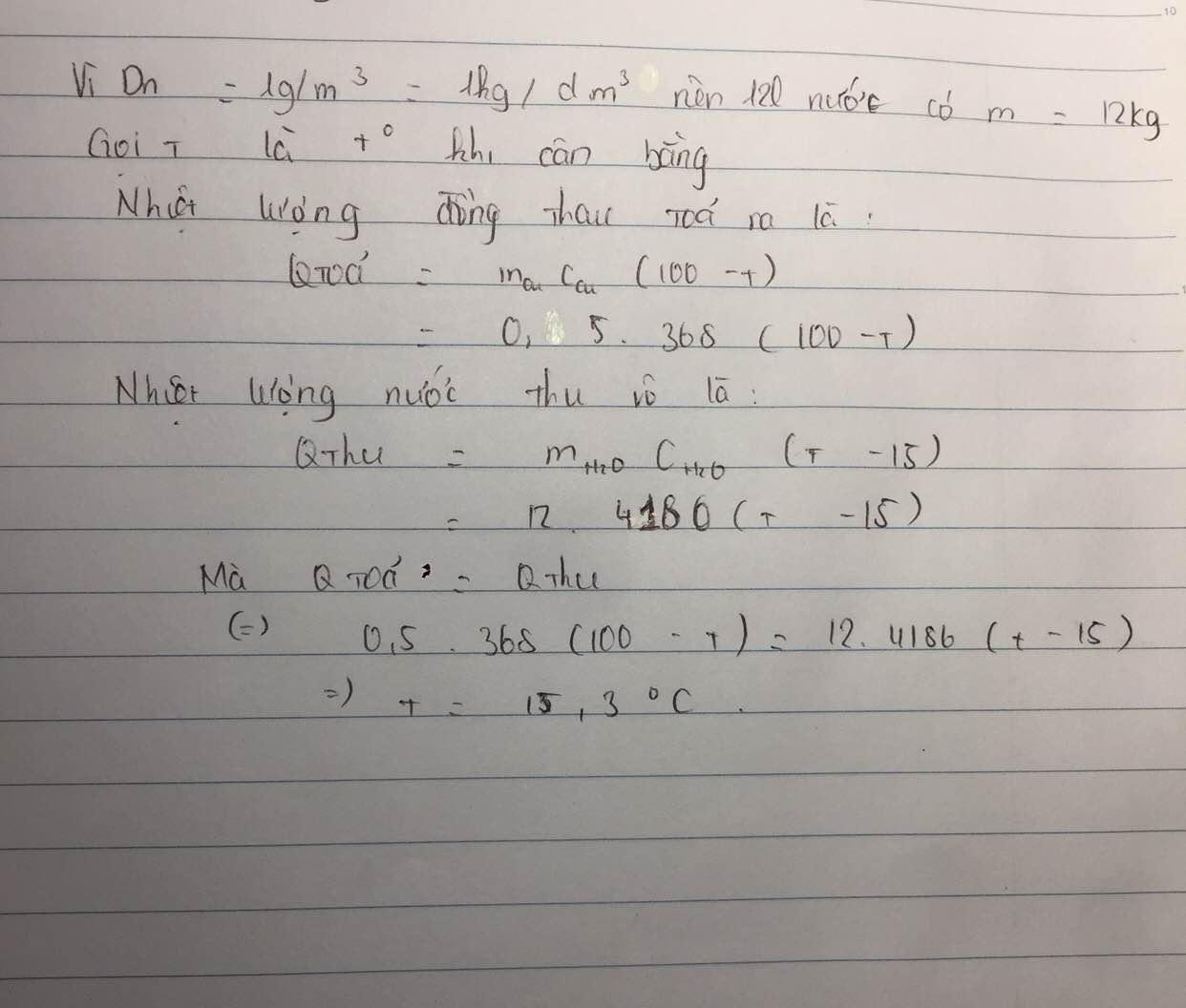
.png)
Tổng quan về bài toán nhiệt học
Bài toán nhiệt học liên quan đến "1 nhiệt lượng kế chứa 2 lít nước" là một dạng bài tập phổ biến trong chương trình vật lý. Nó giúp học sinh hiểu rõ hơn về nguyên lý cân bằng nhiệt, một khái niệm cơ bản và quan trọng trong vật lý nhiệt. Dưới đây là tổng quan chi tiết về bài toán này.
- Đề bài: Đề bài thường yêu cầu tính toán nhiệt độ cuối cùng của nước trong nhiệt lượng kế sau khi cho vào đó một vật có nhiệt độ cao hơn. Bài toán giả định rằng hệ kín, không có sự trao đổi nhiệt với môi trường xung quanh.
- Các yếu tố cần xác định:
Nhiệt độ ban đầu của nước: Thường được cho trước trong đề bài, ví dụ
15^\circ C .Nhiệt độ và khối lượng của vật: Vật được nung nóng tới nhiệt độ nhất định, ví dụ
100^\circ C , và có khối lượng nhất định.Nhiệt dung riêng của các chất: Nhiệt dung riêng của nước và vật phải được biết để tính toán nhiệt lượng.
- Phương pháp giải: Bài toán giải bằng cách áp dụng nguyên lý bảo toàn năng lượng, cụ thể là phương trình cân bằng nhiệt:
Q_{thu} = Q_{tỏa} Nhiệt lượng nước thu vào: Tính bằng công thức
Q_{thu} = m_2 \cdot c_2 \cdot (t - t_2) , trong đóm_2 là khối lượng nước,c_2 là nhiệt dung riêng của nước, vàt_2 là nhiệt độ ban đầu của nước.Nhiệt lượng vật tỏa ra: Tính bằng công thức
Q_{tỏa} = m_1 \cdot c_1 \cdot (t_1 - t) , trong đóm_1 là khối lượng của vật,c_1 là nhiệt dung riêng của vật, vàt_1 là nhiệt độ ban đầu của vật.
Sau đó, bằng cách giải phương trình này, ta sẽ tìm được nhiệt độ cuối cùng
t của hệ sau khi đạt cân bằng nhiệt. - Ý nghĩa của bài toán: Bài toán không chỉ giúp học sinh làm quen với các công thức tính toán nhiệt lượng mà còn nhấn mạnh tầm quan trọng của nguyên lý bảo toàn năng lượng. Đây là cơ sở để hiểu sâu hơn về các quá trình nhiệt động lực học trong các hệ kín và mở.
Công thức và cách tính toán
Khi giải bài toán liên quan đến "1 nhiệt lượng kế chứa 2 lít nước", việc nắm vững công thức và cách tính toán là điều cần thiết. Dưới đây là hướng dẫn chi tiết về các công thức sử dụng và các bước tính toán để tìm ra nhiệt độ cuối cùng sau khi đạt cân bằng nhiệt.
Công thức cân bằng nhiệt
Trong bài toán này, ta sử dụng nguyên lý bảo toàn năng lượng, cụ thể là công thức cân bằng nhiệt:
- Nhiệt lượng nước thu vào:
Công thức tính nhiệt lượng mà nước thu vào khi nhiệt độ của nó tăng từ
t_2 lênt là:Q_{thu} = m_2 \cdot c_2 \cdot (t - t_2) m_2 : khối lượng nước (kg)c_2 : nhiệt dung riêng của nước (J/kg.K), thường là4186 \, J/kg.K t_2 : nhiệt độ ban đầu của nước (°C)t : nhiệt độ cuối cùng của nước sau khi cân bằng nhiệt (°C)
- Nhiệt lượng vật tỏa ra:
Công thức tính nhiệt lượng mà vật tỏa ra khi nhiệt độ của nó giảm từ
t_1 xuốngt là:Q_{tỏa} = m_1 \cdot c_1 \cdot (t_1 - t) m_1 : khối lượng của vật (kg)c_1 : nhiệt dung riêng của vật (J/kg.K)t_1 : nhiệt độ ban đầu của vật (°C)t : nhiệt độ cuối cùng của vật sau khi cân bằng nhiệt (°C)
Cách tính toán
- Xác định các thông số ban đầu: khối lượng và nhiệt độ ban đầu của nước và vật, nhiệt dung riêng của các chất.
- Sử dụng công thức cân bằng nhiệt
Q_{thu} = Q_{tỏa} để thiết lập phương trình: - Giải phương trình trên để tìm nhiệt độ cuối cùng
t sau khi hệ đạt cân bằng nhiệt.
Ví dụ minh họa
Giả sử một nhiệt lượng kế chứa 2 lít nước ở nhiệt độ

Ứng dụng thực tế và bài học rút ra
Bài toán về "1 nhiệt lượng kế chứa 2 lít nước" không chỉ mang tính lý thuyết mà còn có nhiều ứng dụng thực tế quan trọng trong đời sống và công nghiệp. Dưới đây là các ứng dụng và bài học quan trọng rút ra từ việc giải quyết bài toán này.
Ứng dụng thực tế
- Thiết kế hệ thống làm mát và sưởi ấm: Nguyên lý cân bằng nhiệt được áp dụng trong việc thiết kế các hệ thống sưởi ấm và làm mát cho các tòa nhà, nơi cần duy trì nhiệt độ ổn định. Ví dụ, việc tính toán lượng nước cần thiết để làm mát một hệ thống lớn giúp tối ưu hóa hiệu suất và tiết kiệm năng lượng.
- Công nghiệp chế biến thực phẩm: Trong công nghiệp chế biến thực phẩm, việc kiểm soát nhiệt độ trong quá trình nấu nướng và bảo quản rất quan trọng. Bài toán này giúp các kỹ sư xác định chính xác lượng nhiệt cần thiết để đạt được nhiệt độ mong muốn mà không làm hỏng thực phẩm.
- Năng lượng tái tạo: Nguyên lý này cũng được sử dụng trong các hệ thống năng lượng mặt trời, nơi nước được sử dụng như một chất truyền nhiệt. Việc hiểu rõ cách tính toán nhiệt lượng giúp tối ưu hóa việc thu và lưu trữ năng lượng mặt trời.
Bài học rút ra
Tầm quan trọng của nguyên lý bảo toàn năng lượng: Bài toán này nhấn mạnh nguyên lý bảo toàn năng lượng, một quy luật cơ bản trong vật lý. Hiểu rõ nguyên lý này giúp áp dụng vào nhiều lĩnh vực khác nhau như cơ khí, xây dựng, và năng lượng.
Kỹ năng giải quyết vấn đề: Giải bài toán nhiệt học yêu cầu sự tư duy logic và kỹ năng giải quyết vấn đề. Điều này giúp phát triển khả năng phân tích và giải quyết các tình huống thực tế phức tạp.
Ứng dụng trong cuộc sống hàng ngày: Hiểu về nguyên lý nhiệt học giúp con người biết cách tiết kiệm năng lượng, cải thiện hiệu quả sử dụng điện và nước trong gia đình.
Những lỗi thường gặp khi giải bài toán
Khi giải bài toán liên quan đến "1 nhiệt lượng kế chứa 2 lít nước", có nhiều lỗi phổ biến mà học sinh thường mắc phải. Dưới đây là những lỗi thường gặp và cách khắc phục để đạt được kết quả chính xác.
- Nhầm lẫn trong áp dụng công thức cân bằng nhiệt:
Nhiều học sinh nhầm lẫn giữa các công thức tính nhiệt lượng của nước và vật. Điều quan trọng là phải sử dụng đúng công thức:
Q = m \cdot c \cdot \Delta t , trong đó\Delta t là sự chênh lệch nhiệt độ. Để tránh nhầm lẫn, cần xác định rõ nhiệt độ ban đầu và cuối cùng của mỗi chất. - Quên tính toán nhiệt lượng trao đổi với môi trường:
Trong thực tế, hệ không hoàn toàn kín và có thể trao đổi nhiệt với môi trường xung quanh. Nếu không tính đến yếu tố này, kết quả sẽ không chính xác. Để khắc phục, cần xem xét sự ảnh hưởng của nhiệt lượng môi trường trong những bài toán yêu cầu độ chính xác cao.
- Sai sót trong đơn vị đo lường:
Việc sử dụng sai đơn vị (như sử dụng calo thay vì joule, hoặc ngược lại) là lỗi phổ biến. Để tránh lỗi này, hãy đảm bảo rằng tất cả các đơn vị được đồng nhất trước khi tính toán và chuyển đổi đơn vị nếu cần thiết.
- Không xét đến nhiệt dung riêng của dụng cụ:
Khi tính toán nhiệt lượng, nhiều học sinh bỏ qua nhiệt dung riêng của nhiệt lượng kế hoặc các dụng cụ khác, dẫn đến kết quả sai. Trong một số trường hợp, nhiệt dung của dụng cụ có thể ảnh hưởng đáng kể đến kết quả, do đó cần phải tính đến yếu tố này.
- Không kiểm tra lại kết quả:
Sau khi tính toán, nhiều học sinh không kiểm tra lại kết quả, dẫn đến việc bỏ sót các lỗi sai. Để tránh điều này, hãy luôn kiểm tra lại bước cuối cùng, so sánh với điều kiện thực tế để đảm bảo kết quả hợp lý.






.jpg)