Chủ đề vòng tròn lượng giác: Vòng tròn lượng giác là công cụ quan trọng trong toán học, giúp hiểu rõ hơn về các hàm lượng giác và ứng dụng của chúng trong nhiều lĩnh vực. Bài viết này sẽ giúp bạn khám phá cấu trúc, giá trị, và ứng dụng của vòng tròn lượng giác một cách chi tiết và dễ hiểu.
Mục lục
- Vòng Tròn Lượng Giác
- Giới Thiệu Về Vòng Tròn Lượng Giác
- Cấu Trúc Cơ Bản Của Vòng Tròn Lượng Giác
- Các Giá Trị Lượng Giác Trên Vòng Tròn
- Các Góc Đặc Biệt Trên Vòng Tròn Lượng Giác
- Ứng Dụng Của Vòng Tròn Lượng Giác
- YOUTUBE: Khám phá kỹ thuật vòng tròn lượng giác dễ hiểu nhất dành cho học sinh lớp 12 với Thầy VNA. Video giúp bạn nắm vững kiến thức và áp dụng vào bài thi hiệu quả.
Vòng Tròn Lượng Giác
Vòng tròn lượng giác là một công cụ quan trọng trong toán học, đặc biệt là trong lĩnh vực lượng giác. Nó giúp biểu diễn các giá trị của các hàm lượng giác như sin, cos, tan, và cot một cách trực quan và dễ hiểu.
Định Nghĩa
Vòng tròn lượng giác là một đường tròn có bán kính bằng 1 đơn vị, được vẽ trên mặt phẳng tọa độ Oxy với tâm tại gốc tọa độ O. Điểm khởi đầu của vòng tròn này nằm trên trục Ox tại (1, 0).
Các Giá Trị Lượng Giác Cơ Bản
Trên vòng tròn lượng giác, các giá trị lượng giác của một góc θ được xác định như sau:
- Sin(θ): Giá trị tung độ của điểm trên vòng tròn.
- Cos(θ): Giá trị hoành độ của điểm trên vòng tròn.
- Tan(θ): Tỉ số của sin(θ) và cos(θ).
- Cot(θ): Tỉ số của cos(θ) và sin(θ).
Biểu Diễn Trên Vòng Tròn Lượng Giác
Mỗi điểm trên vòng tròn lượng giác tương ứng với một góc θ và có tọa độ (cos(θ), sin(θ)). Các giá trị lượng giác được tính như sau:
- Sin(θ) = y
- Cos(θ) = x
- Tan(θ) = y/x
- Cot(θ) = x/y
Các Giá Trị Đặc Biệt
Các góc đặc biệt và giá trị lượng giác của chúng trên vòng tròn lượng giác:
| Góc (θ) | 0° | 30° | 45° | 60° | 90° |
| Sin(θ) | \( \sin(0^\circ) = 0 \) | \( \sin(30^\circ) = \frac{1}{2} \) | \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \) | \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \) | \( \sin(90^\circ) = 1 \) |
| Cos(θ) | \( \cos(0^\circ) = 1 \) | \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \) | \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \) | \( \cos(60^\circ) = \frac{1}{2} \) | \( \cos(90^\circ) = 0 \) |
Công Thức Lượng Giác
Một số công thức lượng giác quan trọng:
- \( \sin^2(\theta) + \cos^2(\theta) = 1 \)
- \( 1 + \tan^2(\theta) = \sec^2(\theta) \)
- \( 1 + \cot^2(\theta) = \csc^2(\theta) \)
Vòng tròn lượng giác không chỉ là một công cụ học tập mà còn là nền tảng cho nhiều ứng dụng thực tế trong các lĩnh vực khác nhau như vật lý, kỹ thuật và khoa học máy tính.
.png)
Giới Thiệu Về Vòng Tròn Lượng Giác
Vòng tròn lượng giác là một công cụ quan trọng trong toán học, đặc biệt là trong lượng giác. Nó được sử dụng để biểu diễn và tính toán các giá trị của các hàm lượng giác như sin, cos, tan và cot. Vòng tròn này có bán kính bằng 1 và tâm tại gốc tọa độ O trên mặt phẳng tọa độ Oxy.
Cấu Trúc Cơ Bản
Vòng tròn lượng giác có các đặc điểm chính sau:
- Bán kính: 1 đơn vị
- Tâm: Điểm O (0,0)
- Điểm bắt đầu: (1,0) trên trục Ox
Giá Trị Lượng Giác
Trên vòng tròn lượng giác, các giá trị lượng giác của một góc \( \theta \) được xác định như sau:
- Sin(\( \theta \)): Giá trị tung độ của điểm trên vòng tròn
- Cos(\( \theta \)): Giá trị hoành độ của điểm trên vòng tròn
- Tan(\( \theta \)): Tỉ số của sin(\( \theta \)) và cos(\( \theta \))
- Cot(\( \theta \)): Tỉ số của cos(\( \theta \)) và sin(\( \theta \))
Biểu Diễn Trên Vòng Tròn Lượng Giác
Mỗi điểm trên vòng tròn lượng giác tương ứng với một góc \( \theta \) và có tọa độ (cos(\( \theta \)), sin(\( \theta \))). Các giá trị lượng giác được tính như sau:
- \( \sin(\theta) = y \)
- \( \cos(\theta) = x \)
- \( \tan(\theta) = \frac{y}{x} \)
- \( \cot(\theta) = \frac{x}{y} \)
Các Giá Trị Đặc Biệt
Các góc đặc biệt và giá trị lượng giác của chúng trên vòng tròn lượng giác được trình bày dưới đây:
| Góc (\( \theta \)) | 0° | 30° | 45° | 60° | 90° |
| Sin(\( \theta \)) | \( \sin(0^\circ) = 0 \) | \( \sin(30^\circ) = \frac{1}{2} \) | \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \) | \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \) | \( \sin(90^\circ) = 1 \) |
| Cos(\( \theta \)) | \( \cos(0^\circ) = 1 \) | \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \) | \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \) | \( \cos(60^\circ) = \frac{1}{2} \) | \( \cos(90^\circ) = 0 \) |
Công Thức Lượng Giác Quan Trọng
Một số công thức lượng giác quan trọng liên quan đến vòng tròn lượng giác:
- \( \sin^2(\theta) + \cos^2(\theta) = 1 \)
- \( 1 + \tan^2(\theta) = \sec^2(\theta) \)
- \( 1 + \cot^2(\theta) = \csc^2(\theta) \)
Vòng tròn lượng giác không chỉ là một công cụ học tập mà còn là nền tảng cho nhiều ứng dụng thực tế trong các lĩnh vực khác nhau như vật lý, kỹ thuật và khoa học máy tính.
Cấu Trúc Cơ Bản Của Vòng Tròn Lượng Giác
Vòng tròn lượng giác là một công cụ quan trọng trong lượng giác, giúp biểu diễn và tính toán các giá trị của các hàm lượng giác. Dưới đây là cấu trúc cơ bản của vòng tròn lượng giác:
Bán Kính Và Tâm
- Bán kính: 1 đơn vị
- Tâm: Điểm O (0,0) trên mặt phẳng tọa độ Oxy
Trục Ox Và Trục Oy
Trên mặt phẳng tọa độ, trục Ox và trục Oy được sử dụng để xác định vị trí của các điểm trên vòng tròn lượng giác:
- Trục Ox: Trục hoành (trục ngang)
- Trục Oy: Trục tung (trục dọc)
Điểm Bắt Đầu Và Góc
Điểm bắt đầu của vòng tròn lượng giác nằm trên trục Ox tại tọa độ (1,0). Góc \( \theta \) được đo từ trục Ox và có thể có giá trị từ 0° đến 360°.
Các Giá Trị Lượng Giác Trên Vòng Tròn
Các giá trị lượng giác được xác định dựa trên tọa độ của điểm trên vòng tròn lượng giác:
- Sin(\( \theta \)): Giá trị tung độ (y) của điểm
- Cos(\( \theta \)): Giá trị hoành độ (x) của điểm
- Tan(\( \theta \)): Tỉ số của sin(\( \theta \)) và cos(\( \theta \))
- Cot(\( \theta \)): Tỉ số của cos(\( \theta \)) và sin(\( \theta \))
Các Góc Đặc Biệt Trên Vòng Tròn Lượng Giác
Các giá trị lượng giác của các góc đặc biệt trên vòng tròn lượng giác:
| Góc (\( \theta \)) | 0° | 30° | 45° | 60° | 90° |
| Sin(\( \theta \)) | \( \sin(0^\circ) = 0 \) | \( \sin(30^\circ) = \frac{1}{2} \) | \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \) | \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \) | \( \sin(90^\circ) = 1 \) |
| Cos(\( \theta \)) | \( \cos(0^\circ) = 1 \) | \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \) | \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \) | \( \cos(60^\circ) = \frac{1}{2} \) | \( \cos(90^\circ) = 0 \) |
Đường Tròn Đơn Vị
Vòng tròn lượng giác còn được gọi là đường tròn đơn vị vì nó có bán kính bằng 1. Đây là một khái niệm cơ bản trong lượng giác, giúp xác định các giá trị lượng giác một cách trực quan và dễ hiểu.

Các Giá Trị Lượng Giác Trên Vòng Tròn
Vòng tròn lượng giác là công cụ giúp xác định các giá trị của các hàm lượng giác như sin, cos, tan và cot. Dưới đây là các giá trị lượng giác trên vòng tròn lượng giác, được biểu diễn chi tiết:
Giá Trị Sin(\( \theta \))
Giá trị sin(\( \theta \)) được xác định bởi tung độ của điểm trên vòng tròn lượng giác. Dưới đây là các giá trị sin của các góc đặc biệt:
- Sin(0°) = 0
- Sin(30°) = \( \frac{1}{2} \)
- Sin(45°) = \( \frac{\sqrt{2}}{2} \)
- Sin(60°) = \( \frac{\sqrt{3}}{2} \)
- Sin(90°) = 1
Giá Trị Cos(\( \theta \))
Giá trị cos(\( \theta \)) được xác định bởi hoành độ của điểm trên vòng tròn lượng giác. Dưới đây là các giá trị cos của các góc đặc biệt:
- Cos(0°) = 1
- Cos(30°) = \( \frac{\sqrt{3}}{2} \)
- Cos(45°) = \( \frac{\sqrt{2}}{2} \)
- Cos(60°) = \( \frac{1}{2} \)
- Cos(90°) = 0
Giá Trị Tan(\( \theta \))
Giá trị tan(\( \theta \)) được xác định bởi tỉ số giữa sin(\( \theta \)) và cos(\( \theta \)). Dưới đây là các giá trị tan của các góc đặc biệt:
- Tan(0°) = 0
- Tan(30°) = \( \frac{1}{\sqrt{3}} \)
- Tan(45°) = 1
- Tan(60°) = \( \sqrt{3} \)
- Tan(90°) = Không xác định (do cos(90°) = 0)
Giá Trị Cot(\( \theta \))
Giá trị cot(\( \theta \)) được xác định bởi tỉ số giữa cos(\( \theta \)) và sin(\( \theta \)). Dưới đây là các giá trị cot của các góc đặc biệt:
- Cot(0°) = Không xác định (do sin(0°) = 0)
- Cot(30°) = \( \sqrt{3} \)
- Cot(45°) = 1
- Cot(60°) = \( \frac{1}{\sqrt{3}} \)
- Cot(90°) = 0
Các Công Thức Lượng Giác Trên Vòng Tròn
Một số công thức lượng giác quan trọng liên quan đến vòng tròn lượng giác:
- \( \sin^2(\theta) + \cos^2(\theta) = 1 \)
- \( 1 + \tan^2(\theta) = \sec^2(\theta) \)
- \( 1 + \cot^2(\theta) = \csc^2(\theta) \)
Vòng tròn lượng giác cung cấp cách tiếp cận trực quan để hiểu các hàm lượng giác và mối quan hệ giữa chúng, giúp việc học toán trở nên thú vị và dễ hiểu hơn.

Các Góc Đặc Biệt Trên Vòng Tròn Lượng Giác
Trong vòng tròn lượng giác, có một số góc đặc biệt được sử dụng phổ biến do các giá trị lượng giác của chúng dễ nhớ và thường xuất hiện trong các bài toán. Dưới đây là chi tiết về các góc đặc biệt này:
Góc 0° và 360°
Góc 0° và 360° nằm tại điểm (1, 0) trên vòng tròn lượng giác:
- \( \sin(0^\circ) = 0 \)
- \( \cos(0^\circ) = 1 \)
- \( \tan(0^\circ) = 0 \)
- \( \cot(0^\circ) \) không xác định
Góc 30°
Góc 30° nằm tại tọa độ \(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\) trên vòng tròn lượng giác:
- \( \sin(30^\circ) = \frac{1}{2} \)
- \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)
- \( \tan(30^\circ) = \frac{1}{\sqrt{3}} \)
- \( \cot(30^\circ) = \sqrt{3} \)
Góc 45°
Góc 45° nằm tại tọa độ \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)\) trên vòng tròn lượng giác:
- \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \)
- \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \)
- \( \tan(45^\circ) = 1 \)
- \( \cot(45^\circ) = 1 \)
Góc 60°
Góc 60° nằm tại tọa độ \(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\) trên vòng tròn lượng giác:
- \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \)
- \( \cos(60^\circ) = \frac{1}{2} \)
- \( \tan(60^\circ) = \sqrt{3} \)
- \( \cot(60^\circ) = \frac{1}{\sqrt{3}} \)
Góc 90°
Góc 90° nằm tại tọa độ (0, 1) trên vòng tròn lượng giác:
- \( \sin(90^\circ) = 1 \)
- \( \cos(90^\circ) = 0 \)
- \( \tan(90^\circ) \) không xác định (do \( \cos(90^\circ) = 0 \))
- \( \cot(90^\circ) = 0 \)
Bảng Tổng Hợp Các Giá Trị
| Góc (\( \theta \)) | 0° | 30° | 45° | 60° | 90° |
| Sin(\( \theta \)) | \( 0 \) | \( \frac{1}{2} \) | \( \frac{\sqrt{2}}{2} \) | \( \frac{\sqrt{3}}{2} \) | \( 1 \) |
| Cos(\( \theta \)) | \( 1 \) | \( \frac{\sqrt{3}}{2} \) | \( \frac{\sqrt{2}}{2} \) | \( \frac{1}{2} \) | \( 0 \) |
| Tan(\( \theta \)) | \( 0 \) | \( \frac{1}{\sqrt{3}} \) | \( 1 \) | \( \sqrt{3} \) | Không xác định |
| Cot(\( \theta \)) | Không xác định | \( \sqrt{3} \) | \( 1 \) | \( \frac{1}{\sqrt{3}} \) | \( 0 \) |

Ứng Dụng Của Vòng Tròn Lượng Giác
Vòng tròn lượng giác không chỉ là một công cụ toán học quan trọng, mà còn có nhiều ứng dụng thiết thực trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng nổi bật:
Trong Vật Lý
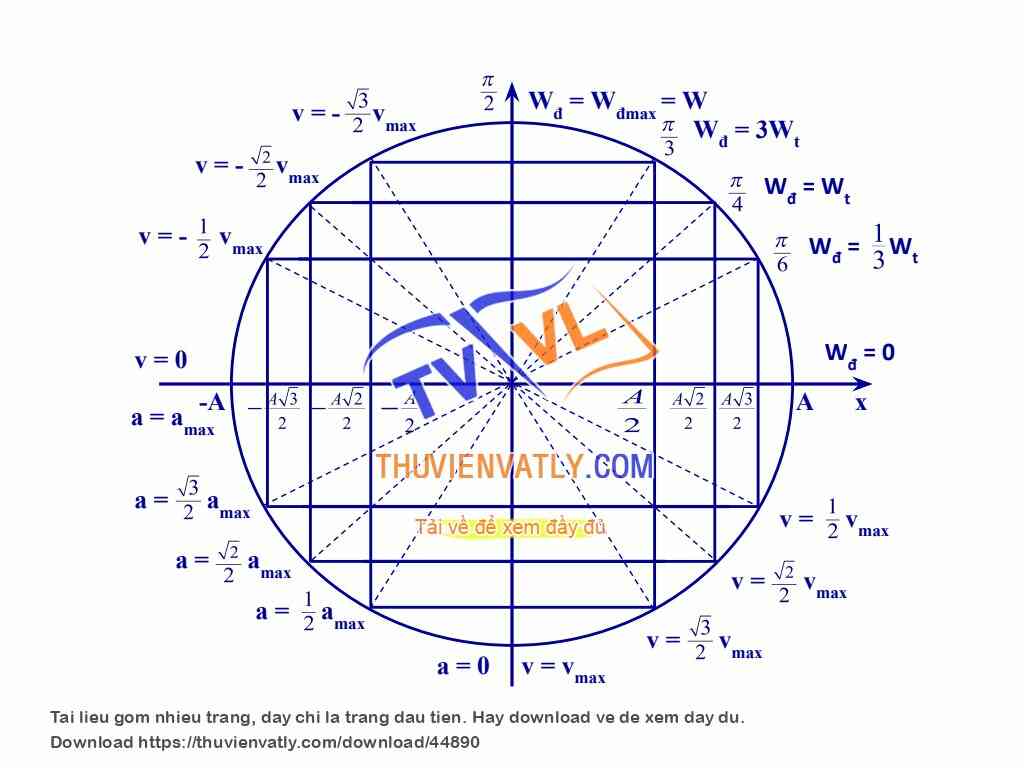
Vòng tròn lượng giác được sử dụng rộng rãi trong vật lý để mô tả các hiện tượng dao động, như dao động điều hòa và sóng. Các giá trị sin(θ) và cos(θ) giúp xác định vị trí và tốc độ của các hạt trong chuyển động tròn và dao động.
- Trong dao động điều hòa, vị trí x và vận tốc v của một vật dao động được biểu diễn qua các công thức:
\[ x = A \cos(\omega t + \phi) \] \[ v = -A \omega \sin(\omega t + \phi) \]
- Trong phân tích sóng, hàm sóng được biểu diễn dưới dạng:
\[ y(x, t) = A \sin(kx - \omega t + \phi) \]
Trong Kỹ Thuật
Vòng tròn lượng giác giúp trong việc thiết kế và phân tích các mạch điện xoay chiều. Các đại lượng như điện áp và dòng điện được biểu diễn dưới dạng hàm sin và cos để thuận tiện trong việc tính toán và phân tích.
- Điện áp và dòng điện trong mạch RLC xoay chiều có dạng:
\[ V(t) = V_0 \cos(\omega t + \phi) \] \[ I(t) = I_0 \cos(\omega t + \phi') \]
- Phương trình cân bằng năng lượng trong mạch:
\[ V_0 \cos(\omega t + \phi) = I_0 Z \cos(\omega t + \phi') \]
Trong Khoa Học Máy Tính
Vòng tròn lượng giác cũng được ứng dụng trong khoa học máy tính, đặc biệt trong lĩnh vực đồ họa máy tính và xử lý hình ảnh. Các phép biến đổi và xoay hình thường sử dụng các hàm sin và cos để tính toán.
- Biến đổi tọa độ khi xoay một điểm (x, y) quanh gốc tọa độ một góc θ:
\[ x' = x \cos(\theta) - y \sin(\theta) \] \[ y' = x \sin(\theta) + y \cos(\theta) \]
- Phép chiếu 3D lên mặt phẳng 2D sử dụng các phép biến đổi lượng giác:
\[ x' = \frac{x}{z} \] \[ y' = \frac{y}{z} \]
Nhờ vào những ứng dụng đa dạng và quan trọng này, vòng tròn lượng giác đã trở thành một công cụ không thể thiếu trong nhiều lĩnh vực khoa học và kỹ thuật



















